THE THEORY OF GRAVITATION
CONTINUATION
Copyright © Harold Aspden, 1960, 1998
This is a reproduction of the text of a booklet written by the author in 1959, published early in 1960. This continuation comprises Chapters 8 and 9 of that work. In the light of his 1998 perspective, some 38 years on from that 1960 effort, the author has added several notes bearing the symbol 
. These may interest science historians who, hopefully, one day will seek to track how the author's theory developed over time.
8
THE GRAVITATIONAL DEFLECTION OF LIGHT
Preliminary Note
The explanation of the deflection of stellar light by the solar gravitational field involves a consideration of a critical field phenomenon predicted by this aether theory.
The energy of a photon may be transmitted as a forced vibration in the aether. This vibration is set up by imparting the energy h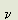
to an aether particle by the action of a force equal to -m(d2x/dt2) which persists while x changes from 0 to xo, where x is xosin2![]()
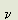. The photon energy velocity is c and as this force does work at the rate -mc(d2x/dt2) the energy of the photon quantity may be found by integrating this expression from t=0 to t=1/4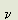. In this way the photon energy is found to be 2mcxo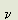. However, this is h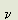, so xo is found to be h/2mc.
Evidently xo is a fundamental constant independent of photon frequency. It represents the amplitude of the displacement of an aether particle as it transmits the photon energy. For the particle acceleration to be equated to the photon driving force the photon field V must balance the electrostatic restoring action due to the displacement of the particle in the continuum. The equation of balance is:
4
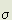ex = Ve ..............(39)
If x is limited to the value xo = h/2mc, V has a limiting value Vo equal to 4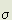xo or 2h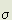/mc.
This aether theory therefore leads to the prediction of a critical field strength which cannot be exceeded in a wave propagation. The critical electric field becomes, from equation (14), hc/16er2, and this may be evaluated from the data presented in Chapter 3. The value of this critical field is 2.21x1013 cgs esu.
This critical electric field is very important in wave-propagation phenomena.
At this point I need to clarify what was in my mind when I wrote this chapter 8. I had come to realise that, in writing about the theory of gravitation, I was trepassing on territory that had been claimed by Einstein enthusiasts. there was zero tolerance of intruders who thought they could contribute to the theory of gravity without building on the Einstein foundation.
I was also, by then, not a part of the academic world, having ventured into employment in industry at the close of my six years at university. My priorites concerned my career and the technological scene. In October 1959 I had committed to conclude my service contract with my employer, giving three months notice, prior to moving to a managerial appointment with IBM. I had three months in which to write The Theory of Gravitation and get it ready for publication prior to shelving my theoretical research interest and concentrating on my task ahead with my new employer.
I knew that academia would show no interest in what I was about to publish, but it gave me satisfaction to get the work on public record.
To head off possible criticism on the point that Einstein's theory offered an explanation of the solar deflection of starlight, whereas my theory offered no such explanation, I addressed that issue as Chapter 8. I was confident that my theory for the photon was sound. I had explained the relationship between the energy quanta and frequency that one sees as a photon 'event'. I had derived a formula for Planck's constant, the constant that governed that link between photon frequency and energy. I had not explained how a photon moves at the speed of light to convey that energy and so, in its transit from a star, grazing past the sun as it converged on body Earth, came to suffer deflection in its transit.
The first thought here was rather obvious. If energy has mass then that photon must exhibit mass and so be subject to gravity. If, as a kind of particle, it travels in close passage as it navigates the region of space occupied by the sun, then it must be deflected. Travelling at the speed of light it would, even by Newtonian theory, be deflected slightly and one could calculate that deflection. It is precisely half the value indicated by einstein's theory. Were photons to travel at half the speed of light, then Newton's theory would suffice. Eddington it seems had championed Einstein's theory owing to the fact that Eddington had made the decisive measurements pertaining to that deflection of satrlight by the solar mass.
Concerning photons I submit that we do not really know how they travel or even if they travel at all. A photon is an event, a transaction occurring at a point in space when a package of energy changes its state in the aether, especially where the transaction involves energy exchange between matter and aether. We know that electromagnetic waves travel at the speed of light but such a wave is a ripple of the sea of energy in the aether so where does the photon feature as motion?
The answer seems to be that it exhibits its presence as a transfer of momentum as if its energy E exerts momentum E/c, where c is the speed of light. Physicists today would do well to wake up to the fact that a photon is an 'event', that the aether is real and that it can be involved in transactions involving momentum and, indeed, angular momentum, but that the deflection of light rays by a gravitational field depends upon the speed of light being affected by the presence of such a field. Einstein says that the speed of light is constant in the vacuum and Einstein then asks us to distort the vacuum so that straight paths of light bend to conform with the distortion of the space metric.
I was somewhat enthusiastic in developing this chapter 8 as part of that effort back in 1959. It was an interesting exercise, but it too was later replaced by something more logical, as one can see from my later publications. All I can add here is to say that I am left with the thought that there may be some maxiumum field intensity that the aether can tolerate before its structure collapses. I now think that has some connection with the very slight radial displacement of aether particles needed to justify the integer nature of the critical number 1843 mentioned in TUTORIAL NOTE No. 8, but I do not see that leading to a breakdown electric field intensity as being as high as the 2.21x1013 esu cgs deduced in this Chapter 8. That is an energy density of 1.94x1025 ergs/cc, equivalent to a mass energy density of 21,600 gm/cc. I point out, incidentally, that if you believe Einstein's theory and subscribe to the belief in Black Holes, then you are in the realm of believing that space (or aether) can tolerate field intensities that transcend even higher levels of concentration of energy density.
Analysis of Electromagnetic Wave-front Energy
An electromagnetic wave, however established, carries energy. If the wave is a plane wave the wave energy per square cm. of the wave must be constant.
Consider two plane boundaries in the wave and separated by a distance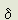 
T. Field flux, whether electric or magnetic, does not cross these boundaries. Thus, if V is the electric field intensity between the boundaries:
V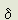 = constant ........(40)
A similar equation involving the magnetic field intensity H also applies.
The field energy per square cm. of the wave is a function of V, H and 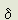T, and the externally induced electric and magnetic fields in which the wave moves. Let F be the externally induced electric field component in the direction of V and M be the externally induced magnetic field component in the direction of H. Then the field energy E of the wave per square cm. between the boundaries of spacing 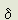T is:
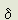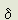E = (T/8)[(F+V)2 - F2] + (T/8)[(M+H)2 - M2] ergs/cc ....(41)
If equations (40) and (41) are differentiated with respect to a parameter y, noting that E is a constant, and that in an electromagnetic wave V=H, it may be verified that:
(1/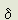T)d(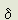T)/dy = (1/V)dF/dy + dM/dy) ......(42)
This equation shows that if the fields F and M are uniform 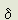T is constant and the wave will therefore not be deflected. However, if F or M varies with y, 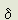T varies with y, showing that in moving a distance 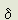T the wave is deflected away from the y direction through an angle d
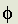equal to (u/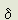T)d(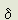T)/dy in time dt, where u is the velocity of the wave. The rate at which the wave is deflected in a non-uniform field is therefore given by combining this result with equation (42) to obtain:
d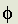/dt = (u/V)(dF/dy + dM/dy) .......(43)
If M is zero or uniform and the field F is strong enough
to polarize the wave, the direction of V may be expected to vary in the plane of the wave so that F is in fact the full intensity of the externally-induced electric field and the energy given by equation (41) is then a minimum. This further means that the vector fields F and V are opposed, and if this fact is applied in the foregoing analysis equation (43) becomes:
d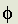/dt = -(u/V)(dF/dy) .......(44)
If F decreases with increasing y the wave is deflected into
the stronger parts of the field.
Deflection of Plane Wave in Passing an Electric Source
Consider the motion of a plane wave past a relatively weak electrostatic charge Q at a point 0. Imagine a point P in the wave travelling in a straight line distant Y from 0. In this case the direction y is as indicated in Fig. 2(a) in the plane of r and P. F at P is:
QY/(X2 + Y2)3/2
and dF/dy is equal to dF/dY, which is found noting that in the plane of the wave front X is constant. Equation (44) shows that the total deflection 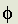is:
-(1/V)
(dF/dy)dX
where the integration is from minus infinity to plus infinity, udt being dX. When 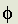is evaluated it is found to be 2Q/VY2.
Deflection of Plane Wave in Passing a Magnetic Source
Imagine the plane wave just considered to pass at a distance Y from a current element idl at 0 as shown in Fig. 2(b). Let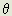 
be the angle between idl and OP, where P is a point in the wave front. At P the magnetic field due to idl is:
mod(idl)mod(sin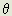/(X2 + Y2)
and in this case 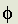may be evaluated as:
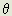(/V)mod(idl)mod(sin)/VY2.
Note that mod(-) implies the modulus or amplitude of a quantity, regardless of its positive or negative significance.
It is of interest to apply this expression to the problem of light deflection by solar gravitation. The effective value of mod(idl) is that attributable to the small gravitational charges orbiting in planes approximately parallel with the earth's planetary orbit. The condition shown in Fig. 2(b) then applies to a ray of light grazing past the sun if Y is the solar radius and mod(idl) is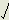 
GMs, where Ms is the solar mass. The mean value of mod(sin 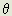is 2/. Thus 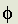is equal to 2GMs/VY2. Taking V as equal to the critical field parameter Vo as already evaluated, 2.21x13 cgs esu, G as 6.66x10-8 cgs, Ms as 2.0x1033 gm, r as 6.95x1011 cm, 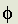is found to be 9.68x10-5 radians or 2.00 seconds of arc.
This result is in agreement with the majority of the results derived from observations during eclipses.
Wave Deflection in the Atom
It is possible to apply equation (44) in an atomic system. Let the atomic number of the atom be Z so that the nuclear charge is Ze. An electron in the K shell will, by simple theory, have an associated orbital radius of rH/Z where rH is the radius of an electron orbit in a Bohr Hydrogen Atom. Let u be its associated wave velocity. Thus the angular velocity d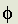/dt of the electron waves in the K shell is given by:
d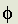/dt = Zu/rH .......(45)
The electric field intensity caused by the charge Ze at the wave orbital radius:
Ze/(rH/Z)2
and the parameter y is distance in a radial direction from the nucleus. Thus:
dF/dy = -2Ze/(rH/Z)2 .......(46)
From equations (44), (45) and(46):
V = 2Z3e/(rH)2 .......(47)
or:
Z3 = V(rH)2/2e .......(48)
The significance of this equation is not immediately apparent. It becomes apparent if one can impose an upper limit on the maximum field intensity of an electromagnetic wave. To fix such a limit will impose a limit on Z. Following this arbitrary suggestion let Vo be the maximum possible value of V and Zmax the maximum possible value of Z. Then, subject to any refinements which a full analysis on Quantum Theory might impose on equation (48):
(Zmax)3 = Vo(rH)2/2e .......(49)
From known data:
e = 4.802x10-10 esu
rH = 5.29x1O-9 cm
Also:
Vo = 2.21x1013 cgs esu
When evaluated from these data and equation (49) Zmax is found to be 86.5. This is very little different from the maximum value of Z found in atoms.
9
THE GYROMAGNETIC RATIO
Although not related to gravitation, one interesting result of this aether theory is the explanation of the anomalous factor 2 found in gyromagnetic phenomena.
Consider the effect of a magnetic field of true strength H in the aether. For simplicity imagine this to be parallel with the axes of rotation of the aether particles and continuum. (The result to be derived may be proved to apply also in a general case.) The field H has the following effects on the radii r and R of the particle and continuum orbits respectively; it causes one radius to increase and the other radius to decrease. Thus:
He(w/c)r + 4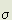e(r+R) = mw2r for particle system
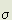-He(w/c)R + 4e(r+R) = mw2R for continuum system
w being the angular frequency of the aether system.
Evidently, in terms of a basic radius ro, and a small increment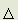 
r:
r = ro + 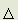r,
and:
R = ro - 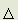r,
where:
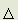r = He(w/c)ro/mw2 .....(50)
The energy involved in the disturbance caused by H is almost wholly kinetic energy and is equally shared between the particle system and the continuum system. It is mw2(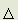r)2 ergs for each element of space including one aether particle. In ergs/cc the energy is found by multiplying by 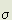/e. Substituting for 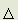r from (50) and m from (14) then shows that the magnetic field energy is:
H2/32 ergs/cc.
Now, the true field H is the difference between the induced field Hi and the aether reaction field Hr. The value of Hr is readily found as 4 times 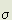/e times the magnetic moment of the elemental space including one aether particle. This is twice that of one particle because the continuum makes an equal contribution. Let the accepted law of the magnetic field induced absolutely by a current be assumed to be in error by the factor K. By accepted law the magnetic moment of the particle will change by (e/c)(w/2)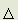r2. From this:
Hr = 2K(4)(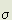/c)(w/2)ror ....(51)
From (14), (50), and (51):
Hr = KH/4 ...........(52)
The directly induced field Hi arising from a current in an electrical apparatus, say, is therefore:
Hi = H(1 - K/4) ............(53)
it is knownthat the magnetic energy accompanying the induced field Hi is (Hi)2/8 ergs/cc. This is also H2/32 ergs/cc. Evidwently Hi is H/2 and K is 2.
It may be concluded that an has, when in orbital motion, twice the magnetic moment normally attributed to it, but when detected as a magnetic field this moment is effectively halved by aether reaction. However, the magnetic moment is not halved in its relation with angular momentum. Hence the anomalous factor 2 of gyromagnetic phenomena.
This note concerning the gyromagnetic ratio has no special connection with the theory of gravitation. I included it because it was my starting point in developing my aether theory. I knew that the inductance energy stored in a magnetic field in a vacuum was recoverable and there just had to be a physical explanation, not one based on empirical formulations which merely recognized the reality of the phenomenon. Physicists had rejected the aether and then had discovered an anomalous factor of 2 in their experimental research concerning angular momentum quanta, electron reaction and ferromagnetic gyromagnetism. I discovered that the factor of 2 was direct evidence of a reaction by something real in the aether and so there was my conviction that the aether was essential as the provider of the storehouse for inductance energy and much more. So I documented this as Chapter 9, and later to simplified the analysis for presentation in my later writings.
10
REFERENCES
[1] CAMPBELL, N. R. Modern Electrical Theory, 2nd Ed. (Camb. Univ. Press), pp.387-8, 1913.
[2] VERONNET, A. Comptes Rendus, v. 188, pp.1380-1, 1929.
[3] WHITTAKER, SIR E. History of the Theories of Aether and Electriciy (Classical Theories) (Nelson), pp.84-7, 1951.
[4] DIRAC, P. A. M. The Principles of Quantum Mechanics, 4th Ed. (Oxford: Clarendon Press), 1958.
[5] NIELSON, C. E. See Appendix III of book by G. Gamow and C. L. Critchfield, Theory of Atomic Nucleus and Energy Sources (Oxford: Clarendon Press), 1949.
[6] EOTVOS, R. v., Math. u. Nat. Ber. aus. Ungarn, viii, p.65, 1891.
[7] ASTON, F. W. Mass-spectra and Isotopes, 1st Ed. (Arnold, London), 1933, pp. 101-2.
[8] CLEMENCE, G. M. Rev. Mod. Phys., v. 19, p.361, 1947.
