return to updates
EXPLAINING
return to hompage
the
ELLIPSE
by Miles Mathis
The Problem
All experiments and observations have confirmed that Kepler's equations are correct and that the shape of the orbit is indeed an ellipse, as he told us. Most physicists have been content to leave it at that. If you are an engineer and you have equations and a diagram, you have all you really need. If you are a physics teacher and you have equations and a diagram, you are well prepared: you can answer almost any question that is likely to come up. But in my paper on Celestial Mechanics, I showed that the accelerations and velocities in the elliptical orbit were impossible to explain with the gravitational field. That is to say, we have the correct equations, the correct shape, but the wrong mechanics. We have left the equations and the diagram with no foundation for almost four centuries! The proposed and accepted kinematics and dynamics, studied closely, cannot support the motions in the field. Since physics is supposed to be a mechanical explanation of natural phenomena, we have a very real problem here. We have titled this part of physics "celestial mechanics", but we have left out the mechanics almost entirely. This should be a concern to all real scientists, and not just theorists or philosophers, either. If your field does not explain your equations or your diagrams, you are not lacking in metaphysics, you are lacking in physics. What we currently have is a set of equations hanging from sky hooks. A set of free-floating equations is not physics, it is heuristics.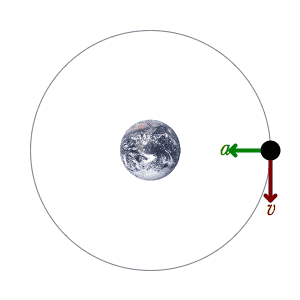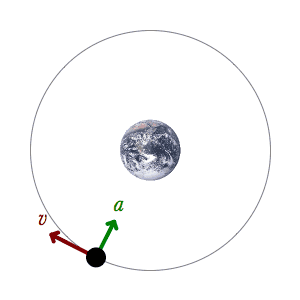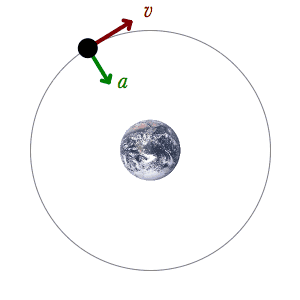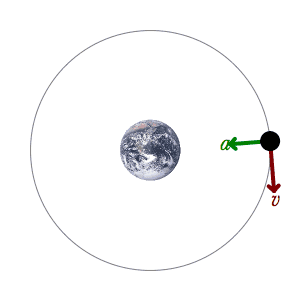
All orbits, whether elliptical or circular, are assumed by historical and current theory to be composed of only two motions, a centripetal acceleration caused by gravity, and a velocity due to the orbiter’s “innate motion.” This term “innate motion” was most famously used by Newton, and it has never been updated. It is still considered to be the velocity that the orbiter carried into the orbit from prior forces or interactions. It may also be a motion caused by the formation of a nebula or solar disc, but it cannot be caused by the gravitational field of the current orbit. Why? Because there is no mechanism to impart tangential velocity by a gravitational field. Both Newton and Einstein agreed on this. Einstein’s tensor calculus shows unambiguously that there is no force at a perpendicular to the field, and Einstein stated it in plain words. How could there be? The force field is generated from the center of the field, and there is no possible way to generate a perpendicular force from the center of a spherical or elliptical gravitational field.
The orbital velocity of an orbiter at any point in the orbit is the vector addition of the two independent motions; that is to say, the centripetal acceleration at that point in the field and the perpendicular velocity, which is a constant. If you study the diagram below, you will find that this can be shown quite simply. The orbiter must retain its innate motion throughout the orbit, no matter the shape of the orbit. If it did not, then its innate motion would dissipate. If it dissipated, the orbit would not be stable. Therefore, the orbiter always retains its innate motion over each and every differential. If we take the two most important differentials, those at perihelion and aphelion, and compare them, we find something astonishing. The tangential velocities due to innate motion are equal, meaning that the velocity tangent to the ellipse is the same in both places. But the accelerations are vastly different, due to the gravitational field. And yet the ellipse shows the same curvature at both places. The ellipse is a symmetrical shape, just like the circle.
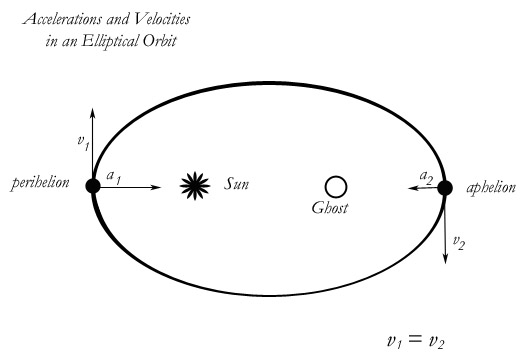
This is physically impossible. Using the given motions, the ellipse is impossible to explain. The logical creation of an ellipse requires forces from both foci, but one of our foci is empty. It is a ghost. Every explanation I have seen of the elliptical orbit, including—perhaps most famously—Feynman’s explanation, uses the visualization of string and thumbtacks (see diagram above, below title). But this visualization requires two foci. It cannot work with an ellipse and only one focus.
I know that many will cringe that I have claimed in my illustration that v1 = v2. Don't I know that the orbital velocity varies in an elliptical orbit? Yes I do. Once more, my velocities are not orbital velocities, they are tangential velocities. I refer the readers who do not comprehend my point to my paper on circular motion. In a nutshell, the orbital velocity describes an arc or curved line. It is the vector addition of the tangential velocity and the centripetal acceleration, over the same interval. Newton first created this analysis, and I do not disagree with it. Unfortunately, contemporary physics has forgotten his distinction. It usually conflates orbital velocity and tangential velocity. But the tangential velocity does not curve. It is a straight-line vector with its tail at the tangent. It does not curve even at the limit. It only gets very small at the limit. By going to the limit or to Newton's ultimate interval we do not curve the tangential velocity, we straighten out the arc. That is to say, we straighten out the orbital velocity so that we can apply a vector addition to it, putting it in the same equation as the straight tangential velocity.
Am I saying that celestial bodies cannot be in elliptical orbits? No. I am saying that these elliptical orbits cannot be explained with the theory we currently have. What we currently have is a very complex set of equations for determining the orbits we actually see. This is called heuristics. The theory underlying this math, which is called the theory of the gravitational field, cannot explain the most basic math it contains. From the time of Newton and Kepler, the foundational theory of ellipses has existed with a ghost in it. That is to say, a huge theoretical hole. It is time to fill that hole.
Current theory attempts to plaster up that hole by summing the closed circuit, whether it is circular or elliptical, showing that everything resolves. But this proves nothing, since they cannot help but resolve. We are talking about a closed circuit, by definition. It would be very surprising if the sums did not resolve. What I am talking about here is differentials. Just like in orbital theory, the differentials betray huge holes in the theory. These differentials can be summed, to show a circuit, but the variance they contain cannot be explained by the gravitational field or the innate motion.
To make the ellipse work, you have to vary not only the orbital velocity, but also the tangential velocity. To get the correct shape and curvature to the orbit, you have to vary the object's innate motion. But the object's innate motion cannot vary. The object is not self-propelled. It cannot cause forces upon itself, for the convenience of theorists or diagrams. Celestial bodies have one innate motion, and only one, and it cannot vary.
[This section added May 2008] Some have still not understood my point here, so I am adding another diagram. 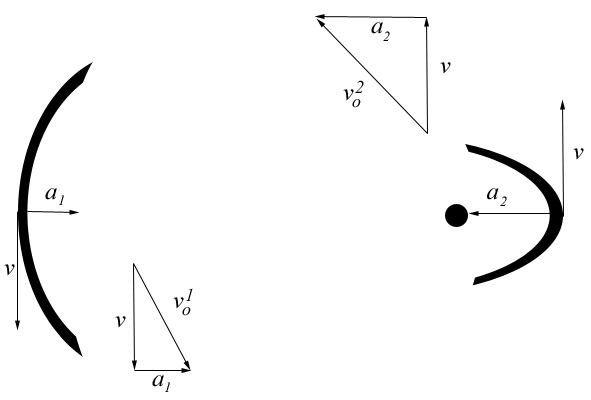
In this diagram you can see that the vectors given by Newton and Kepler demand more curvature at perihelion than aphelion. When the orbiter is nearer the sun, its orbital path must show more curvature. The vector v is a constant, by definition or axiom, so the variance in a must determine the curvature of the path at any point. I have also diagrammed the orbital velocities, vo, to show how they are found by adding the other two vectors. As you can see, the orbital velocity at perihelion is indeed greater than at aphelion, as shown by the length of that vector. But the tangential or perpendicular velocities at all points on the orbital path must be the same. Therefore, we must find the curvatures as I have drawn them here. Now, perhaps, you can more clearly see that these two "ends" of the ellipse cannot be made to meet up. You cannot have greater curvature at perihelion and lesser curvature at aphelion and draw any shape that will meet up. This is my central thesis in this paper. I am not claiming that Kepler's or Newton's math is wrong. I am not claiming that planets do not draw ellipses. Empirically we know that both the equations and the orbital shapes are correct. The problem is with the underlying mechanics. The gravitational field, as it is currently defined, cannot support the shape or the equations. Since the shape and the equations are known to be correct from experiment, we must create a unified field that explains them. I do that in the next section and in my Unified Field paper.
The Solution
Fortunately, the solution is just as simple as the problem. It has been overlooked for centuries, but that does not mean it must be esoteric. It only means that the problem was hidden for a long time. Newton hid the problem so cunningly that no one has detected it since his time.
The solution is that the orbital field is a two-force field. It is not just determined by gravity. Therefore any orbiter must be exhibiting at least three basic motions. The two above, and one other. This other is a motion due to the combined E/M fields of the orbiter and the object orbited. In this case, the Sun and the Earth. The force created by the E/M fields is a repulsive force, like that between two protons. It is therefore a negative vector compared to the gravitational field, which is an attractive field. And so the total field described by gravity and E/M is a differential of the two. In the end, you subtract the E/M acceleration from the acceleration due to gravity.
This explains the ellipse because the E/M repulsive force increases as the objects get nearer. As the gravitational acceleration gets bigger, so does the repulsive acceleration due to E/M.
We have a balancing of forces. This not only explains the varying shape of the orbit, from circle to ellipse to parabola, it explains the correctability of the orbit. It explains why we don’t often find orbiters crashing into primaries. It explains how we had a ghost in the other focus of the ellipse: the ghost was inhabited by the E/M field.
This also explains the cause of the ellipse. It has never been understood why some orbits were elliptical and some were nearly circular. Various explanations have been offered, from initial spin, to various perturbations, to an initial angle at intersection to the field. My theory would explain the ellipse in the orbit of captured orbiters by simply showing that the orbiter intersected the field too far from its center. The captured orbiter does not have to intersect the field at just the right distance. It can be captured over a large range of distances, since if it is captured too far away, it will just be thrown into ellipse.
This makes my analysis the opposite of the current analysis. I showed in my Celestial Mechanics paper that current analysis explains the circular orbit as the orbiter intersecting the field at a distance where the two motions balance. By this theory, the ellipse would have to be caused by an initial intersecting radius that was smaller than this balancing radius. I have a diagram in that paper that proves this. If the orbiter is captured at aphelion, for instance, it would begin to get closer to the Sun due to the shape of the ellipse. This could only be explained by showing that the centripetal acceleration overpowered the tangential velocity.
But my orbit is the balancing of three motions, not two. Therefore, the circular orbit would be caused by an intersecting radius where the gravitational and E/M fields balanced. So that to create the ellipse, you would go farther away, not closer. Remember that the E/M field drops off faster than the gravity field. Gravity decreases as 1/R2. E/M decreases as 1/R4. If you go farther out, gravity overpowers E/M and the orbiter immediately begins to move closer to the Sun.
To show this, I will gloss the capture for an elliptical orbit: 1) the orbiter intersects the field too far away for a circular orbit—meaning that it is beyond the balancing of the three independent motions, but travelling slow enough that the acceleration due to gravity captures it; 2) since the centripetal acceleration initially overpowers the E/M field and the tangential velocity, the orbiter begins to circle closer to the center; 3) but as it does so, the E/M field increases, keeping the orbiter from crashing; 4) the orbiter reaches a minimum orbital distance where the E/M field and the gravitational field [almost] balance; 5) since the orbiter in question is a very large body and the E/M field is made up of very small bodies, the momentum of the orbiter will actually have taken it a small distance inside the balancing radius; 6) the object being slightly below its radius where the two forces balance, the E/M field force is, for a short time, greater than the gravitational force; 7) this creates a very small slingshot effect; 8) due to this effect, the orbiter’s momentum carries it outside the balancing radius; 9) if the initial intersection angle was not too steep—so that we didn’t get too far under the balancing radius—then we are back to 1). Otherwise we create a parabola instead of an ellipse, and the object escapes a semi-stable orbit.
The only step that needs further comment, I think, is step 5. Another way to state step 5 is that the E/M field is a physical object that is much more fluid than the planet that intersects it. The planet is a solid object whose own E/M field is quite rigid. But the central E/M field contains more space and less structure, so that its effect on a solid object will be delayed in this instance.
A useful visualization is to compare the planet intersecting the E/M field to a heavy wooden ball being thrown into deep water. Because the ball is wood, we know that the water will float it—that is, repel it. But if you give the ball enough initial velocity, it will dive into the water to a certain depth before the water begins to reject it. A planet is like a very heavy wooden ball, and the E/M field is like a very weak water. The planet therefore dives to a great depth before the E/M field overcomes the initial momentum. The planet may be “under water” for months. But at last the E/M field floats it.
The buoyancy of the wooden ball determines it force of rejection by the water, and the E/M field of the planet determines its force of rejection by the central field. Its E/M field is determined by its mass and its density.
The visualization is analogous in another way. When the water finally rejects the wooden ball, the ball pops out of the water, often to a measurable height. You have probably experienced this at the swimming pool. If you hold a plastic, air-filled ball under water and then let it go, it will explode out of the water and jump a foot or more into the air. The E/M field of the Sun ultimately rejects the planet in the same way. This is the slingshot effect.
Current theory makes use of this same slingshot effect, but it does not explain the foundational mechanics of it. Current theory tries to build the same unbalanced field as I have, so that the orbiter goes into a sort of gravitational “well.” But this unbalance cannot be created with a single field. Any close analysis explodes the whole theory. Current theory has the right effects and the right ideas, it just has the wrong forces. The gravitational field by itself cannot create the forces required to display the effects and curvatures and differentials that are required. To create unbalanced forces and slingshot effects and correctable orbits, you have to have two major intersecting fields. The innate motion is not a field. It is just a simple velocity. In this way it is a constant. It cannot create all the effects that current theory wants to give to the orbit.
Implications
The greatest implication of all this is that Newton’s fundamental gravitational equation must be reconsidered. The force in the equation F = GMm/r2 can no longer be considered the expression of a single field. The equation still works, but F must now be understood as the differential between the gravitational field and the E/M field. It is a compound field. All the accelerations we measure are the result of both fields working simultaneously to yield a total force and a total acceleration. This total acceleration is a vector addition of the two constituent accelerations.
A smaller implication is that comets might now be shown to burn not simply from solar radiation, but from the E/M field. That is, the tails of the comet would be produced mainly by electrical considerations. The comet is on electrical fire. This may seem at first to be splitting hairs, but it is not. Solar radiation is not thought to be radiation from an E/M field. It is thought to be ions created as by-products of nuclear fusion. But E/M fields are created independently of nuclear fusion. The Sun would have a powerful E/M field even if it were not a giant nuclear reactor. Therefore, it may be the E/M field that is the main cause for the spectacular effects of comets.
You may now see the simple unified field equations for the three-body problem (Sun, Earth, Moon) in my newest paper on Lagrange Points. Using the charge field, I am able to show that the Moon is in fact hitting these points of field balance. This proves my assertions in this paper.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.