return to homepage WHY DOES A RAINBOW Abstract: I will show that the current answer is wrong on all levels. Using Alexander's band and stunning photographic evidence, I will prove that the curve of the rainbow is caused by a heretofore unseen phenomenon, one both simple and intuitive. Alexander's band is an image on a screen of a layer of the corona of the Sun.
This one was a "toughie". I had to do a little looking. I had plenty of info on "why" rainbows, but not so much on "why round" rainbows. This is from Hewitt, Suchocki, and Hewitt's Conceptual Physical Science, second edition, p 293. It is published by Addison, Wesley, Longman, copyright1999.
(You might try your local library if you wish to learn more; and if you want to see the really good diagrams that Mr. Hewitt draws.) Anyway, here goes: Why does the light dispersed by the raindrops form a bow? The answer to this involves a bit of geometry. First of all, a rainbow is not the flat
two-dimensional arc it appears to be. It appears flat for the same reason a spherical burst of fireworks high in the sky appears as a disk-because of a lack of distance cues. The rainbow you see is actually a three-dimensional cone with the tip (apex) at your eye. Consider a glass cone,the shape of those paper cones you sometimes see at drinking fountains. If you held the tip of such a glass cone against your eye, what would you see? You would see the glass as a circle. Likewise with a rainbow. All the drops that disperse the rainbow's light toward you lie in the shape of a cone—a cone of different layers with drops that deflect red to your eye on the outside, orange beneath the red, yellow beneath the orange, and so on all the way to violet on the inner conical surface. The thicker the region containing the
water drops, the thicker conical edge that you look through, and the more vivid the rainbow.
The reason a rainbow is a smooth curve is because it is the *angle* between the light incident on a raindrop, and the light exiting the raindrop, that determines what color is seen. And, as you note, it
also depends on the fact that raindrops are, on average, roughly spherical. The path from sun to raindrop to viewer's eye includes the angle, and all the raindrops located so that the angle has a
particular value, will contribute to a particular color of the rainbow. This might be difficult for a child to visualize, but it is a simple geometrical notion that you can demonstrate with a coat hanger.
Here is a maybe more detail than you really want about how it works:
return to updates
CURVE DOWN?

This will be the first in a series on color and refraction. Optics is a very difficult field, still only partially understood. We are told that Newton was right about almost everything, but here again that is false. Newton was sometimes partially correct and sometimes completely wrong, but he was rarely completely right. Even Newton updated by Young and Fresnel and Helmholtz and Maxwell and all the rest is not correct or complete, as we will see here.
First, let us look at the current answer. We go first to Wikipedia, which seems to have a manufractured (a typo, but I like it, stet, and expect to see me use it again) answer for just about everything. But this time we get zilch. Not even a bad answer or a link to a bad answer. We are linked to UCAR, the Center for Atmospheric Research, but we get almost nothing on the curve. Only this: “The rainbow is thus a circle of angular radius 42 degrees, centered on the antisolar point.” Ditto with the link to Walter Lewin: nothing good about the curve. So we do our own search. We find a couple of bad answers at “Ask a Scientist” at the US Dept. of Energy:
A rainbow is round because the process is based on angles. Light from the sun hits the little water droplets after a rain. The water droplets act like little prisms. Different colors are sent out at different angles. The sun must be behind you. Imagine a narrow triangle. The narrow angle is at the water drop. One side points toward the sun. One side points toward your eye. The drops for which this device works form a circle. The center of this circle lines up with you and the sun. If the Earth were not in the way, a rainbow would be a complete circle. This is why you can never find "the golden pot at the end of the rainbow". A rainbow is really a complete circle.
Dr. Ken Mellendorf Physics Instructor Illinois Central College
Your cone of vision that intersects the cloud of drops that creates your rainbow is different from that of a person next to you. So when a friend says, "Look at the pretty rainbow," you can reply, "Okay, move aside so I can see it too." Everybody sees his or her own personal rainbow. I hope that casts "light" on your rainbow query.
Martha Croll
First, some background: a ray of light that hits the middle of the raindrop is partially reflected and partially transmitted. The reflected part goes back directly toward the source; the transmitted
part goes through the raindrop and is partially reflected at the back surface. Again the reflected part goes back directly toward the source; the transmitted part leaves the raindrop and we don't care
about it anymore. That ray that reflected from the back surface is now heading back toward the front surface, where the partial-reflection thing will happen again—many times, in fact. On each round trip,
some light will be transmitted through the front surface back to the source.
Second bit of background: What if the light ray hits off center? Then things get very interesting. First, the surface of the raindrop acts as a prism, since the light is incident at an angle, and the light will be refracted (its path will be bent) as it passes through the surface. Second, the first reflection from the back surface will not be in the same place as the second reflection from the back surface; the light will sort of bounce around within the drop, reflecting here and there in a very predictable manner and sequence.
Third bit of background: each reflection from the back surface will make its own rainbow. Normally, you can only see the first-reflection rainbow, and maybe a faint suggestion of the second-reflection rainbow (at a different angle).
Fourth bit of background: The angle through which a light ray is bent as it passes through the air-water surface depends on the index of refraction of the water (and the air). The index of refraction of
water is different for different colors of light. This is because electrons in the water molecules are tuned, like guitar strings, and a light ray tries to vibrate them at the frequency (color) of the
light ray. Light rays that are nearer in frequency to the electron's "tune" are affected differently—i.e., they see a different index of refraction—i.e., they are slowed down by a different amount, and
therefore refracted by a different angle—than light rays farther away in frequency.
So a light ray hitting the raindrop off center will be refracted, and part of it will exit the raindrop at an angle that depends on how off-center the incident ray was. In fact, as the ray hits further
and further off center, the exiting ray will make a greater and greater angle with the incident ray—up to a point. There is a maximum exit angle, which corresponds to a certain off-center distance, and
the exiting light is concentrated near this maximum angle, because the variation of exit angle with off-center distance is smallest near this angle. You can demonstrate this with a laser and a cylinder of
something clear. The maximum exit angle depends on the color of light because the refraction angle generally depends on the color.
Tim Mooney
Then we find an answer seemingly cobbled from these at Yahoo Answers: “The reason why the rainbow is curved is because all the angles in the water drop have to be just right for the drop to send some sunlight to you, standing on the ground. So, with the sun *behind* you, only those water droplets that have the same angle formed by you, the drop, and the sun (this angle happens to be approximately 42 degrees) will contribute to the rainbow. Other droplets send their light somewhere else, and if you move to a different location, new droplets are needed to make the rainbow you see in the new location. This is why you can’t go to the end of a rainbow to find the mythical leprechauns and pots of gold; anywhere you stand, the rainbow is formed by faraway drops of water reflecting and bending sunlight. The rainbow is curved because the set of all the raindrops that have the right angle between you, the drop, and the sun lie on a cone pointing at the sun with you at one tip.”
All the other answers I could find on the internet were variations of these, so I suppose this is state-of-the-art. So let us analyze these before we give the right answer. Dr. Mellendorf's only sentence that addresses the question is this one: “The drops for which this device works form a circle.” That is a statement of fact, though, not a statement of cause. The question asked is “why is the circle formed?” Because the device forms a circle is not an answer.
Ms. Croll's answer is also a dodge. She says the rainbow curves because it is part of a cone, but that is just renaming a curve a cone. What causes the cone?
Tim Mooney wins the award for misdirection, however. We get six paragraphs of “background information” and no answer at all to the question asked. We knew we were in trouble the moment he put “angle” in unneeded quotations. He tries to imply that the curve is caused by the curve of the individual raindrop, but that is clearly illogical. Then he tells us that it might be difficult for a child to visualize, but that you can demonstrate it with a coat hanger. Only one problem: he forgets to demonstrate anything to us with a coat hanger.
The Yahoo answer may be from Mr. Mooney as well, since we again get “behind” in unnecessary quotations of the same kind. And again, most of this is misdirection about raindrops, which are the current cause of the refraction, but not of the curve. The only relevant sentence is the last one, about the cone. But as with Ms. Croll, that is a description, not a answer. Substituting a cone for a curve does not tell us anything.
I have to say that it is sad that these scientists would even bother to post such clearly deficient and defective answers. Do they really imagine that they have addressed the question? Does the Dept. of Energy think it is good PR to have physics seen in this state of undress?
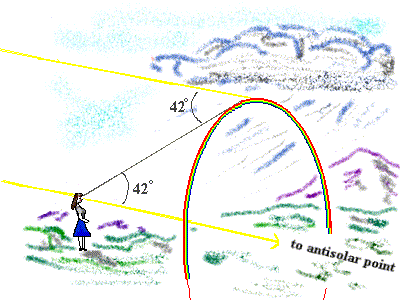
This is the illustration at UCAR. It was developed from Descartes' answer from 1637. That's right, we are still using basic rainbow theory from 1637. The problem is that this angle of 42o goes to infinity. Why is the rainbow drawn that distance from the lady rather than three feet away from her or ten miles away? These people will say that rainbows can vary in their apparent distance, but according to this diagram, we should see huge rainbows many miles away. The clouds themselves, when at a 42o angle, should cause rainbows. Current theory has a limit on the Sun's height in the sky, which limits other factors, but what is the limit on the rainbow's size? The height of the Sun and the 42o angle provide no size limit.
An even bigger problem than that comes when we look more closely at this theory. UCAR has drawn green below red, but they admit that shorter wavelengths are refracted by different raindrops than the raindrops that refract red. Red and green can't be coming from the same raindrop, and they realize that. If all the colors we see were split by each raindrop, then red would be below green. So they tell us the lower raindrops refract green to us and the upper ones refract red. That appears to be an ingenious solution until you remember that patches of rain don't come in sheets a single drop wide. Look at this illustration I made:
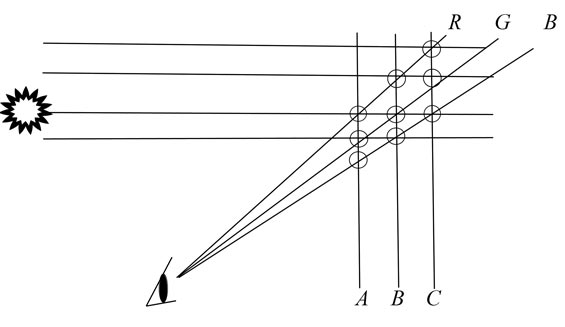
Where do we see the rainbow? At position A, B, or C? I will be told, "All three, and the rainbow will just be more saturated." Maybe, but that doesn't explain why rainbows often look very saturated with very little rain in the air. Just look at the picture under title, chosen by Wiki to adorn its own page due to the saturation of the bow. But the bow is just as saturated near the ground, where there appears to be very little moisture. It is clear as a bell down there. The saturation seems to be a function of something else. It also doesn't explain why rainbows are so steady. They don't shimmer or wobble and the face doesn't shift even in high wind. It is easy to postulate a leading wall of moisture that is not flat to us, due to wind or other turbulence, or evaporation, or other effects. If the position is determined by the leading raindrops, shouldn't we see a tilted band under some conditions? Why is the rainbow so steady, even under turbulent conditions like a thunderstorm? And why does it always appear flat to us, as if it is aligned to gravity? I have no doubt that the color is created by the medium, but the position of the color seems strangely undetermined by the medium.
A greater problem for the standard model occurs when we look at the curve. Imagine instead a rainbow with no curve. Just draw a rainband in the sky with no curve. Can this be explained with their 42o rule? Yes. All the red raindrops at the top can be explained as having a 42o refraction. You just have to postulate that the outer raindrops are a bit further away. Why is that impossible, according to them? Why should all the raindrops you see be equidistant from you? Can we not imagine sheets of rain that set up this way relative to you and your Sun position? Of course we can. So why do we never see straight rainbands? What they have done is sneak in an assumption as an explanation. They say, “If the refraction angle has to be constant, and if the distance to the raindrops has to be constant, then we will see a curve.” Yes, true, but that doesn't explain why the distance to raindrops has to be constant. Yes, we appear to see the raindrops in a cone of visibility, equidistant from our eye. But again, why? A description is not an explanation.

Here's a photo that proves the current explanation is false. You can see that the photographer has turned to take a picture of just one leg of the rainbow. The Sun is no longer behind the photographer, relative to the “cone of sight”, and this is clear from looking at the light on the mountain. The Sun is now on the left shoulder of the photographer. Ask yourself this: if the image of the rainbow is dependent on the cone of sight, shouldn't the image be flat to the viewer on both ends, and not just in the middle? As we turn to focus on one of the legs, we should see it flat to us. Instead, we see it flat to the Sun. The whole rainbow is always in single plane, no matter how close or far away it is to us, or how much we zoom in on one leg with a camera. This despite what we are told about the rainbow being different for every viewer. But that is a big lie, one you can test yourself very easily. The rainbow isn't even different for you as your turn your head or as you move around. You can walk quite a distance relative to a rainbow, and it doesn't change at all. It stays right where it was, as if it is part of the landscape. This fact conflicts most aggressively with the current explanation, since the rainbow is supposed to be a function of your cone of sight. If the rainbow is a function of the cone of sight, the rainbow should move against the far background as you move. But it doesn't. This is one of the great mysteries of rainbows, and always has been, and yet the historical explanation utterly ignores it. No, you can't walk over and find where the rainbow hits the ground, without making the rainbow disappear, but you can certainly "uncenter" yourself to it. If you couldn't, then the two legs of the rainbow would move as you moved. They don't. In many regards, the rainbow acts like an image on a screen. Your own position is generally set, but not definitely set. If the rainbow was a function of your light cone, as we are told, then your position would be definitely set.
Which brings up another theory-ender. You don't really have a cone of sight, do you? What you have, according to this strange theory of sight, is a sphere of sight all around you. All points equidistant from you form a sphere. The cone they are talking about is formed when this sphere intersects a plane. The sheet of rain is supposed to be this plane intersecting your sphere, creating a cone. Unfortunately, that would mean the sheet of rain would have to be at a 90o angle to you and the Sun. Otherwise you would see one leg of the rainbow nearer to you. The current guardians of theory will say, no, it only means the raindrops you see as colored are in that plane, but that brings us back to the earlier problem: why would you see rainbows or raindrops only in this cone of visibility, when you don't see other things that way? You don't see only things that are equidistant from you. You can resolve lots of different objects at lots of different distances, so this cone of visibility is just a mirage. They are still trying to sneak in an assumption as an explanation. They get you thinking that to see something, all the photons have to arrive simulaneously, but that is absurd.
I like to say that problems are not as hard as they seem, but I will admit that this one is deep. It didn't come to me on the first try. In fact, it didn't come to me until I looked closely at Alexander's band. Alexander's band is the dark band between two rainbows, named for Alexander of Aphrodisias, the Aristotelian of the third century AD. Many rainbows are doubled, with the outer rainbow opposite in color to the inner. This is now explained as due to a second path of refraction inside raindrops, but I will show in other papers that this is also false. At any rate, the dark band in between the two rainbows is explained as a gap between the two phenomena: that is, as a gap between the raindrops refracting with three inner bounces and those refracting with four inner bounces. Unfortunately, like all else, this explanation of the dark is completely illogical. We are told the band is dark because we are seeing refracted light above and below, coming from the raindrops. But this would only explain increased light within the rainbow itself. It cannot explain increased darkness in the band. We only have to look at real rainbows to see that the light variations around the rainbow are not explained by the current theory.
In fact, the explanation of the darkness of Alexander's band and the brightness inside the rainbow is some of the worst of current theory. As for the latter, we are told by Wiki:
The minimum deviation angle for the primary bow is 137.5o. Light can be deviated up to 180o, causing it to be reflected right back to the observer. Light which is deviated at intermediate angles brightens the inside of the rainbow.
Amazing how versatile those little raindrops are. They always manage to explain everything with a new refraction or reflection angle. So, accordingto current theory, at the center of the rainbow the raindrops are reflecting light right back to us. Then, from 180o to about 140o, we also get get a “deviation” that causes white light, and this deviation causes just as much brightness as a straight reflection (since the rainbow is not brightest right at the center: the whole center is equally bright). At about 140o, we start to get color. From 138o to 129o we get no refraction, reflection, or deviation, or at least none that can reach our eye. From 129o to 127o we get a four-breaker refraction inside the raindrop, causing a reverse rainbow, and then below 127o we again get some brightening, but not as much as from 140o to 180o.
It is beyond belief that such pathetic theories are ever published or taken seriously by anyone. Leaving aside the question of color creation for later, we only need to ask why a spherical raindrop would increase brightness by reflecting or deviating light to us from 140o to 180o, and from 127o to 0o, but would not send us any extra light from 138o to 129o. Interference is supposed to be creating supernumerary arcs, as we will see in the next paper, but Alexander's band is not supposed to be an interference phenomenon. It is supposed to be caused by “minimum deviation.” As evidence of this, we are sent again to Descartes, and his 138o red refraction (same as 42o, measured from the other side). That is the minimum deviation of the inner color band, as you see in the illustration from Wiki.

Problem is, that is just a limit of this three-bounce refraction, it is not a limit of all other possible reflections and deviations. Light can reflect off the back of the raindrop in a single bounce at any angle, depending on where we let it hit in the illustration. We can also get reflection or deviation in a two-bounce hit, scattering light at any angle. So this minimum deviation is just a misdirection. There is no minimum deviation at 138o, except for the color red as created by three bounces.
A further problem is that current theory is basically using scattering theory to explain color creation, but the two are opposite. If a single raindrop can cause so many different refractions, including a one-bounce reflection at any angle from 90o to 180o, a two-bounce refraction over a wide range of angles, a three-bounce refraction over many angles, and a four-bounce refraction over many angles (plus other bounces) what we have is scattering, not refraction or “deviation.” As is known, scattering causes white light, not colored light. So this theory of three and four-bounce refraction isn't even consistent. This becomes really clear when they start pushing the theory to explain Alexander's band. They are trying to make the same raindrops cause brightening via scattering, and cause color splitting via refraction. Unfortunately, media don't work like that. The prism doesn't work like that. A prism doesn't brighten. It either reflects or refracts, but cannot do both in the same position. If it is reflecting, it is not refracting, and vice versa. For this reason alone, the raindrops cannot be the cause of brightening. If they were scattering, they wouldn't be causing color, since scattering turns color to white. And they can't scatter at some angles and cause color at other angles, via the same turning of forward light.
The same applies to the minimum deviation for the outer color band. The current theory tries to create a limit there, but there is none, except (perhaps) for four-bounce color. At all angles, we will have an equal probability for single bounce and double bounce reflection or deviation or scattering or whatever you want to call it. So this part of the theory is garbage.
Just look at this quote from the same page at Wiki:
The minimum deviation angle for the secondary bow is about 230o. The fact that this angle is greater than 180° makes the secondary bow an inside-out version of the primary. Its colors are reversed, and light which is deviated at greater angles brightens the sky outside the bow.
What? Just consult the last illustration above, which is right next to this text at Wiki. You can see the angles of "deviation" yourself. You may ask the author why angles of 230o to 232o create color, but angles of 232+ create brightening. How can one angle be defined as refraction and the angle right next to it be defined as scattering? This is the same mechanism! Shouldn't the angles above violet create ultraviolet, according to any logical theory based on the historical models? Ultraviolet rays would not brighten the sky. Since we can't see them, they would actually darken it, comparatively.
Also notice that, using the current theory, Alexander's band is explained as the natural brightness of the sky, without any brightening by the raindrops. But either my photos or any study of rainbows will show that isn't true. Alexander's band is the darkest part of the sky, and we can confirm that by looking at parts of the sky where no rain is in the air. The moisture “wall” is never running across the whole sky in front of us, from horizon to horizon. How could it be? So it is usually easy to compare Alexander's band to parts of the sky unaffected by the rain. That fact is, Alexander's band is not a lack of brightening, it is a darkening. It is darker than inside the inner band and outside the outer band, so that the current theory doesn't even address the facts. Even if the theory had a leg to stand on, as a matter of refracting angles, it wouldn't explain the facts. Alexander's band is not a gap between brightening, it is a darkening.

To explain the band, we need to return to the photos. Here is a beautiful picture showing that the whole inside of the rainbow is lighter than the rest of the sky. This is an extreme example, but all rainbows show this effect to some degree. The darker the rest of the sky is, the easier it is to see the difference in brightness. Here's another stunning example. You really feel the Sun inside the bow, and have no problem believing that this is reflection of the Sun itself. Not a "creation" of the Sun, but an actual "picture" of the Sun and its corona.

Here's a closeup that shows the amazing contrast inside and outside:

And in this photo we see that the sky outside the two bands is also lighter than the Alexander band, though not nearly as light as inside the rainbow.
I will show in an upcoming paper that this lesser contrast is what makes the outer rainbow less vibrant in color. Yes, it is the bands of dark and light that cause the rainbow, not the rainbow that causes the bands of dark and light. But to prove that I have to first show that the circles of dark and light are caused by some so-far unseen phenomenon. If these circles of light and dark are causing the rainbow, as I claim, what is causing the circles of dark and light?
It turns out that Descartes was completely wrong. Rainbows are not caused by a refraction of sunlight by a triple bounce inside a raindrop. Nor are the colors split in the way claimed, with red being refracted by different drops than violet. That is all just a fairly ingenious myth.
The Sun is commonly behind us at certain angles, it is true, but that is because the rainbow is primarily a reflection of the Sun cast upon a field of moisture or dense atmosphere from behind. A bright patch in the far sky acts as a reflector, and the dense atmosphere in between acts as a screen. We are seeing a cast image of the Sun in the sky. In this way, we see that Alexander's band is actually an image of the least luminous band of the Solar corona. Study this picture:

On the right side of the image (straight from Wikipedia), peaking at about 2 o'clock, you can easily see a band formed. The band goes all the way around, but it is clearest on the right side. About halfway to the edge of the corona, you have a fairly distinct line, separating the corona in half. It is darker inside this band, and lighter outside. The corona is at a much higher temperature, and this is commonly known. What is less commonly known is that the corona, despite this higher temperature, is not as luminous as the Sun itself. It is not as luminous simply because it is less dense. The Sun has more atoms, and therefore more emission. Therefore, we have three layers here: the brightest is the Sun, then a darker layer, then a brighter layer. Just as with the rainbow. And if you study the width of the middle layer here, you will find it matches the relative width of Alexander's band!
In this picture, we find that the middle band of the Sun is about ¼ the radius, or a little less. If the band is 1 inch, the radius is 4.25 inches, according to my measurement. This is exactly the width of Alexander's band, relative to the radius of the inner rainbow. Measuring from the other rainbow photos I have published here (and from others on the web), I get 8.5 to 2, which is a match. Alexander's band is not caused by a gap between refractions, it is caused by the Sun's corona layers. Here is another photo that shows it,

though it shows it clearly only on top. We can't see the ring all the way around in this rather poor photo, but we can see the width of the band. Again, it is precisely the right width to match Alexander's band.

The Moon also has an Alexander's band, as we see here, although it appears to be wider than the Sun's and is probably caused in a different way. But since the Moon is also lit by the Sun, we can assume that the Moon's band is also a reflection of the Sun's corona. The band is probably widened by the curvature of the surface of the Moon. You can see all three brightnesses, with the Moon itself included. The darkness of Alexander's band could not be clearer. You can even see larger bands that cause higher order rainbows. We see similar effects around the Sun in similar conditions, so higher order rainbows are probably caused in a similar way.
Here is a third corona image from the Sun, for good measure. Again, you can see Alexander's band most clearly from 12 to 4 o'clock, and can even see how it affects the large flare at 4 o'clock.
Of course this means that the curve of the rainbow is just the curve of the Sun itself. We are seeing an image of the Sun cast on the atmosphere. This is why it is higher or lower depending on the height of the Sun. But it has nothing to do with your cone of sight. The rainbow is larger or smaller, appearing closer to you or further away, depending on the relative positions of the bright reflecting place way in front of you and of the patch of thick atmosphere that is acting as a screen.
As proof of this, let us look at some more photos. Photos are wonderful, and honestly, it is photos that have allowed me to get beyond Descartes and the rest of ossified theory in this case. I am not standing on the shoulders of giants so much as standing on the shoulders of photographers (all of whom I would like to thank). Let's start with several that show the reflecting point in the background. Pictures from falls are great for this.

This first one is a close-up, but the rainbow here is actually not very big. It is close and small. This is because the reflection point behind is not far away: it is the bright area seen in the picture, the white in the falls. White means the light is being reflected back, and it is reflecting an image of the Sun. Notice the rainbow is most vibrant near the white. The colors fade as we move away from the white reflecting area. That is why the photographer focused on this leg of the rainbow. The white is the reflecting surface, and the mist is the screen. The image is cast from behind, and then the image goes through the mist. So the mist acts as both screen and prism. The mist does cause the color like the prism, but it does not bounce it three times using the Descartes process. I will show the creation of color in my next paper; I am only showing the creation of the curve here, remember.

Here's another from Niagara. You will say that the least color is seen with the most white behind, but here that is due to a lack of mist up high, at the top of the arc. The mist isn't up there, so it doesn't matter how white the light is behind. The thing to notice is that the rainbow is not very big, and that is because the white reflecting area isn't very far away from the rainbow. The image hasn't had room to spread out after the reflection.

Here's one that proves my point very nicely. We can almost see the body of the Sun inside the rainbow, and we can see the white reflecting point on the far horizon. That is why the rainbow is so large: the distance between the reflecting point and the bow is great, allowing for the image to expand before it reaches the screen.

Now look closely at this one (again straight from Wiki), which I have posted as large as possible. We have such detail here we can even see the radial details of the corona, where the rays shoot out. We can clearly see a line moving out from the center. How does the current theory explain this? It can't. No theory of interference can explain radial lines. This is like a slide of the Sun's corona projected onto a screen in the sky.
Yes, the rainbow is, first and foremost, a rear-projected image of the Sun onto a screen of moisture in the atmosphere. This layer of moisture acts as both a screen to cast the image upon, and a refracting medium to cause the color. But the light must come from behind, because the light must travel through the medium in order to be refracted. Just as light must pass through a prism, light must pass through the layer of moisture, in this case coming toward us from behind the screen.
This is of paramount importance, because it shows that current theory has never been an analogue of prism theory, although it claimed to be. Prisms do not refract light back toward a viewer. With the prism, refraction was always defined as the turning of light at an angle of less than 90o. A reversal of light, or a turning at an angle of greater than 90o was called a reflection. A prism can do both. It can reflect with no color, or refract with color. But it can't do both through the same face. If you are receiving refraction, you cannot be also be receiving reflection. And the prism never scatters or brightens.
Rainbow theory, as taken from Descartes, has tried to sell this three-bounce, 138o turn as a prismatic refraction, causing a color split. But technically, this turn is a refraction plus a double reflection from surfaces, not a triple refraction. And technically, reflections do not cause color separation. It is not clear that Descartes' description was ever viable, even according to classical theory. And according to current photon theory, as updated by people like Feynman, refraction does not just happen at surfaces. The math of refraction is limited by surfaces, but cannot be explained by surfaces alone. It is an interaction with matter itself, and matter itself is not confined to surfaces. Therefore, the raindrop cannot be considered to be an empty sphere, with reflective surfaces. The raindrop may be able to both reflect and refract, as the prism can, but it is not clear that it can refract backwards. If it reflects from a back surface, it doesn't split into color; and if it splits into color, using both front and back surfaces, like a prism, then the light should pass through the back surface, being bent but not reflected.
My mechanics bypasses all that, since according to the evidence I have presented, the light IS refracted, but since it comes from behind the sheet of rain, the refraction is a bending, not a reflection. This matches prism theory and data. The whole sheet of moisture acts as the medium, not just a single drop.
That said, my color creation will be just as revolutionary as my curve creation, through bands of dark and light. I have shown that these bands of dark and light cause the rainbow and the colors, not the reverse. The curved bands are primary, and the color is secondary. In my next paper, I will show that Goethe was right in his contradiction of Newton. In many effects, it is not material edges that cause diffraction or refraction, it is darkness and lightness alone. I will prove this by showing you that we can look at bands of black and white and grey on a flat computer screen through a prism, and obtain color splits from that. This will require a complete rewrite of not just rainbow theory, but color theory in general. I will rehabilitate Goethe's theory of color, but I will do so without deposing Newton. As I have done before in other debates, I will be able to synthesize both sides, taking the best parts of both.
[Thanks again to all the great photographers whose work I used. I didn't find photo credits on the web, or I found web monikers. If you want a photo credit for your work, just drop me an email and I will add a tag to this paper, and also a link to your own page if you like.]
Go to part 2, where I show how color is split (and where I also rehabilitate Goethe and his optics).
Go to part 3, where I show a new explanation for the white rainbow, or fog bow.