Condensed Intro Tesla Coils

Contents: Eric Dollard's condensed intro int the Tesla coil, without the included Tesla patent.

html version here: http://www.tuks.nl/pdf/Eric_Dollard_Document_Collection/OCR_in_progress/Condensed_Intro_to_Tesla_Coil/html/Condensed_Intro_Tesla_Coils.html

OCR pdf version: http://www.tuks.nl/pdf/Eric_Dollard_Document_Collection/OCR_in_progress/Condensed_Intro_to_Tesla_Coil/Condensed_Intro_Tesla_Coils_OCR.pdf

Doc version: http://www.tuks.nl/pdf/Eric_Dollard_Document_Collection/OCR_in_progress/Condensed_Intro_to_Tesla_Coil/Condensed_Intro_Tesla_Coils.doc

I removed the Tesla patents, because these can be found on the net already in digital form:

http://www.tfcbooks.com/patents/0645576.htm http://www.tfcbooks.com/patents/1119732.htm

---

PRIMARY AND SECONDARY COILS Experimental Unit at Bolinas, California, 1981 DISCLAIMER: This material was written early in the project and is in need of extensive revision. Pages 1-16 result from experimental investig­ations and theoretical considera­tions while at my lab in the Marconi Wireless Building (R.C.A.), at Bolinas, California, from 1980-1981. Pages 22-25 are taken from reference (2) and adapted for relation to Tesla Coil waves. Pages 25-31 are taken from reference (3) and serve as an illustration of how the Tesla Magnifying Trans­mitter can extract energy from the Earth's resonant electric field. Eric P. Dollard March 22, 1986

P.O. BOX 429 • GARBERVILLE, CA 95440-0429 • U.S.A. THE TESLA TRANSFORMER At the turn of the century Tesla was in the process of devising a means of wireless power transmission. The transmission involved the generation of longitudinal ether waves. Whether Tesla accomplished this is not known, but the idea was considered by other notables

• such as Kelvin and Maxwell. Kelvin considered it possible to

generate "longitudinal waves in the luminiferous ether" thru the phenomena of displacement current (capacity current). He goes on to indicate his feeling that these waves must be faster than light, as the longitudinal waves in a steel rod move with much greater velocity than the transverse waves. Tesla claims that the waves from his transformer propagate atthe velocity of light. It is interesting to note that the velocity measured on the Tesla coil is alsogreater than the velocity of: light, but this does appear to be a phase velocity rather than a group velocity. In his writings Tesla indicates some seemingly impossible phenomena surround the emanations from the spherical terminal capacity, and I have determined these to be true by experiment. One is that the power gradient (poynting vector) is in the same axis as the dielectric flux gradient. The other is the slow forma­tion of a conductive area surrounding the sphere that is not ionic in nature (in other words is not a spark or glow discharge). Contrary to popular relief, the Tesla transformer is not a

• See reference 6.

steady state device but is a magnifier of transient phenomena. Also it does not behave like a L. C. network nor a transmission line, but more like a unique type of wave guide. If all parts of the system are designed properly the EMF and hence dielectric flux jumps from zero to an enormous value almost instantaneously, thereby producing an almost inconceivable displacement current into space. The transformer is then basically a device for rapidly discharging the capacitor bank nearly instantly into free space, producing an enormous dielectric shock wave similar to a sonic boom. Because the dissipation of the transformer is for all practical purposes negligible, the energy keeps increasing at a linear rate per cycle of oscillation, thereby accumulating a gigantic quantity of electrical energy. (A form of laser action may be possible.) In order for the transformer to resonate with the planet the energy storage in the active region that grows around the sphere terminal must equal the conjugate energy storage of the earth, a stiff requirement. It is interesting to note that dielectric breakdown in this active region grow into a log periodic form based on X2-X=1 as the log base. This will be recognised as the trancendental PHI or the Golden Ratio. In glow discharges the ions of metallic elements form stable spheres of diameter inverse to the atomic weight of the element involved. The transformer's principals of operation are as follows: The first requirement is the sudden collapse of an energy field thereby producing a sudden impulse of energy, second is the

transforming properties of the odd harmonic ordered single wire delay line (coil) which allow for the production of enormous E.M.F. and M.M.F., and third, the dielectric phenomena surrounding the free space capacity terminal. 1) The formation of the energy impulse involves the discharge of a capacitor with the highest practical stored energy into an impedance (inductive) of the lowest practical value, and the discharge path is coupled to an energy supply through a negative resistance device. This negative resistance is classically a spark discharge, but a superior plasma device needs to be developed to enhance efficiency. Under optimal conditions the exponent of oscillation amplitude will be positive over a sustained period of time. The net result of this system is the production of an extreme impulse of M.M.F. of great. An alternate method is the discharge of an inductor of the highest practical stored energy into a circuit of the lowerst practical admittance, thereby pro­ducing an enormous impulse of E.M.F. of great 2) The energy impulse generated by the aforementioned methods is then coupled into a pair of single wire transmission systems. Through induction a strong travelling wave is formed. Due to the impedance transforming properties of the odd (, etc) order line, the E.M.F. of the wave is converted into lightning magnitudes, still retaining the extreme d/dt of the initial discharge. The capacitive discharge method of impulse generation is Tesla's favorite, but Steinmetz shows that inductive discharges will also work. The capacitor contains the initial energy of the oscillating system. The buss from the capacitors to the primary loop should have a negligible transient impedance. The capacitors should be of the bolt on vacuum type, however, the unique dielectric properties of water might be of advantage as capacitor plates. The capacitors must be in symmetrical arrangement with the primary coil. The primary must be of one turn only and exhibit the lowest practical impulse reactance. Tesla indicates the proper length of the primary conductor to be, where n is a harmonic number convenient for the size of the unit and K is unspecified. Also unspecified is if this value is free osc. disconnected from the capacitors or is LC dependent. The transmission network consists of twosingle wire transmission systems of negligible radiation loss. The first of these is called the secondary coil. The next is called the "extra coil" by Tesla, but henceforth will be called the "Tesla Coil". This network or line is typically absent in most units purporting to be Tesla transformers. The secondary coil serves as a matching network between the wave generating primary loop and the Tesla coil. The magnetic coupling factor "k" between the PRI and SEC coils is typically 20%. Negligible magnetic coupling should exist between the secondary and Tesla coils. The function of the secondary is three fold. The first is the transforming of the primary M.M.F. pulse into an abrupt travelling electric wave. Second, to provide a constant potential constant current transformation for good voltage regulation at the output terminal of the Tesla coil, and third is to match the drive impedance of the Tesla coil to the drive impedance of the earth. *(next page) The secondary coil is of a low characteristic impedance of the value This low impedance requires it to be of high self capacity. This capacity is best facilitated by flat spiral coils of wide strip, or by short coils of wide strip, or by short coils of wide strip wound edgewise. The diameter of the secondary must be very nearly that of the primary loop. 3. Connected to this secondary coil is an additional coil, the Tesla coil. This is where the magnification properties are most pronounced. This line or coil is also long however, it must possess the minimum possible self capacity, resulting in the highest possible characteristic impedance, thereby facilitating the greatest possible magnification of E.M.F. by the relation

 •

The self capacity of the coil is minimum when the diameter is equal to length, roughlyper centimeter of diameter. The velocity of propagation alone this coil istimes the velocity of light due to the distributed shunt capacity. This results in pronounced capacity effects when the coil is operated higher in frequency than resonance. It will discharge a rate much faster than the angular velocity of free oscillation, producing explosive phenomena- The self capacity of the terminal sphere brings the frequency of OSC down to that of light velocity by acting as a shunt capacitor load across the coil. There ;an be considerable energy radiation from the capacity terminal. Steinmetz equations show a power factor as high as 40% is possible. Dielectric radiation from the Tesla coil itself must be minimized.

• It should be noted that the primary acts as a halfwave, therefore exhibiting no impedance transforming properties.

FIG 26

10 This is achieved by concentric configuration with the primary/ secondary system thereby enclosing its dielectric flux. The potential gradient along the Tesla coil is approximately a step function due to the phase displacement of the input impulse's harmonics, however, the velocity of the higher ordered overtones become proportionate to frequency if the self capacity becomes significant, thereby distorting this gradient which assumes equal velocity for all overtones. Consider the table. Frequency Coil Length in Degrees Input Pulse Degrees Fo 90° 0° 3FO 270° (-90°) 0° 5F0 450° (+90°) 0° 7F0 630° (-90°) 0° The harmonics of the time function impulse are all in phase, however, the harmonics of the space function are all out of phase and is therefore a step function. The coil can be considered a form of differentiator. Hence the gradient along the coil is abrupt at the last few degrees of coil length but small elsewhere along coil (see Fig. 2) . The last turns of the coil must be insulated accordingly, it would seem possible the gradient to continue to increase beyond the dielectric terminal!* By facilitating the last few degrees in a lead from coil to terminal, the gradient can be made to appear along the lead rather than in the coil, minimizing capacity and flashov

• EMF then also becomes greater farther from terminal, possible reaching astronomical magnitudes.

11 problems. The dielectric radiation from this lead will be small as it is immersed in the sphere's flux. No data exists as to the ratio of the size of the sphere and earth. The complete Tesla transformer is shown in Fig. 3. The electrical length is 36 0 degrees at the fundamental of oscillation. The earth connection must have negligible transient impedance, a star radial system preferred. The earth terminal is the M.M.F. counterpart to the E.M.F. capacity terminal. Like the capacity terminal, it is quite possible that the magnetic gradient and force will increase as the wave penetrates the earth. Hence the 5 sections of the Tesla transformer: 1. Earth 2. Primary system/ power supply 3. Secondary wave coil 4. Tesla or magnification coil 5. Dielectric antenna It should be. born in mind that Tesla designed this system for the transmission of electric waves.* This is hardly desirable for lab work as severe damage to unprotected apparatus and electrical interference can result. To confine the energy an image coil (180° shift) must be connected to the earth terminal. Making this arrangement in a horseshoe configuration produces intense dielectric flux and displacement current that is quite useful for plasma work. Due to the immense difficulties surrounding the spark device, a simple method and one of much greater control is shunt feed of the primary network by an A.M. radio transmitter of special design such as the unit at building number one. Due to the high impedance

• The theories of radio at that time considered transmission thru existing lines of force or "ether tensions".

FIG 3

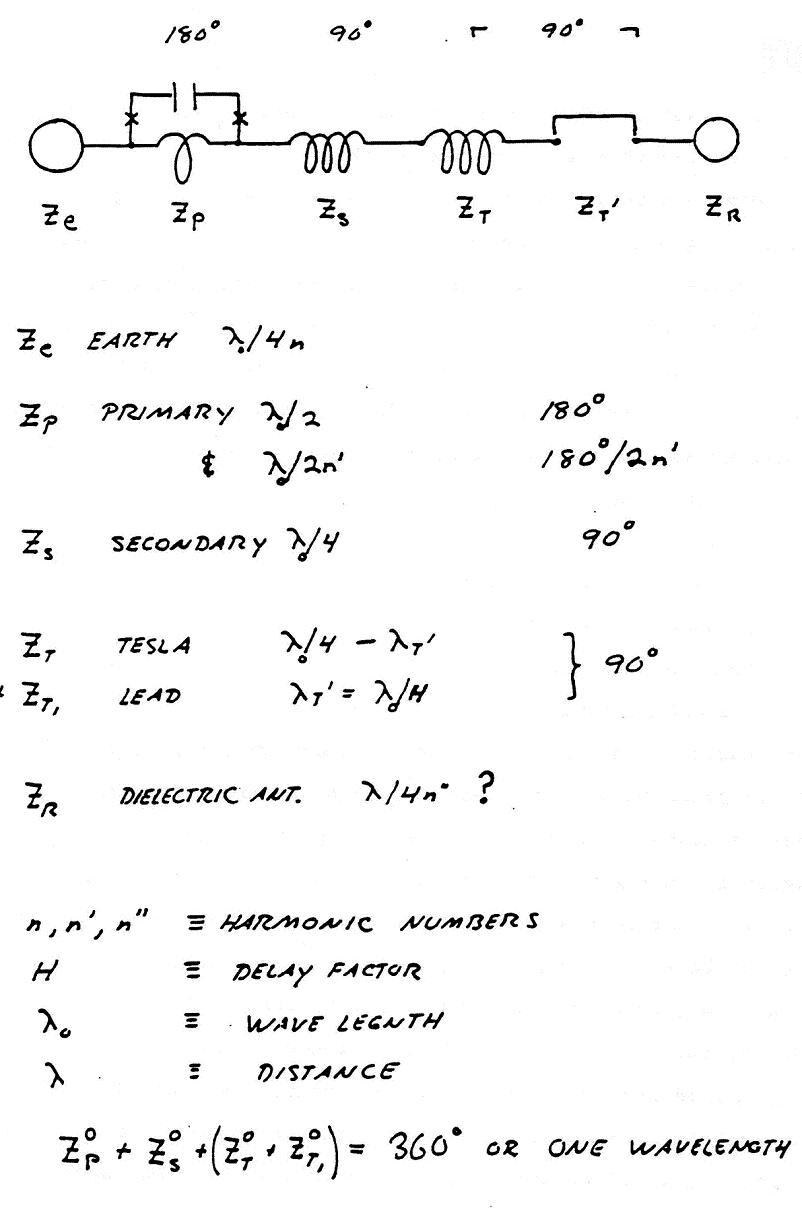
FIG 4 offered by the primary resonator the impedance effective of the tubes must be high and therefore must operate at high anode voltages. The electron emission however, must also be high, necessitates large cathodes and temperatures. High anode and large electron emission are usually of inverse relation in available vacuum tubes. Special pulse modulator vacuum tubes must be used. Hydrogen thyratrons might operate satisfactorily at low frequencies where the 1 microsecond deionization time will not hinder commutation. The most effective device for shunt feed may be the multipactor tube due to its strong negative resistance effects, but it is not clear if it will operate below 1000KC with much efficiency. By the utilization of the aforementioned devices a much improved field is developed at the transformer output with regard to stability. This I have found desirable for the production of stable plasma formations. However, I have not noticed the "jamming together of electrons" unless the spark method is used as the rate of rise of EMF is much greater by the spark method. Perhaps the multipactor will operate comparatively but strong impulses do not seem possible with shunt methods. For stability of certain plasma effects AFC may be required. (See Fig. 5) The image coil system exhibits strong discriminator effects and thereby facilitates the formation of an error signal to the V.C.O. As to physical construction the primary should be sheet copper of great conductor width and large loop area. Large surface is required as the skin effect is total with impulses. Large width also minimizes inductance allowing for larger capacitors and more

Fig 5 - Setup for plasma work - Scope shows size of plasma with respect to time. rapid discharge and hence high impulse strength. In opposition to this required inductive reduction is the need for a large area due to the flashover and coupling requirements. Hence a balance has to be established between the need for minimum inductance for rapid discharge and for a large magnetic field, resulting in large inductance. The formula for inductance (rationalized) is L=area/width. Tesla indicates that the copper weight of the secondary must equal that of the primary for maximum efficiency. This of course goes along with standard transformer theory but it must be remembered that the depth of penetration of waves into conductors is microscopic for impulses. This copper requirement must be modified to equal surface area rather than weight. As to the use of water for capacitor conductors Tesla gives no reason. It would seem that this is done for the sake of simplicity and/or is a holdover from the Leyden jar. (Remember he began this in 1890). However, water has many curious dielectric properties that may be essential in operation. By theory, for maximum discharge velocity the dielectric must be a vacuum. Analysis (See Fig. 6) The oscillating coil differs from the transmission line on account of turn to turn capacity and distributed mutual induction. The presence of series capacity causes the coil to respond as a capacitor network (with no inductive effect) towards abrupt impulses and angular velocities greater than the angular velocity of free oscillation.

Fig 6 The voltage distribution along the coil at the first instant depends on the factor . Cg= capacity to ground, Cs= capacity from end to end. The greater a, the greater the concentration of voltage at the feed end of the coil. The maximum voltage per unit length is equal to a times the voltage of uniform distribution. a is a small fractional value with Tesla coils. The greater the d/dt or the greater the gradient of voltage. If the impulse has a long tail the phenomena will be as described but followed by a damped oscillation. (OSC) By impressing a sustained oscillation, and if the coil has a small dissipation constant u, the voltage will continue to increase indefinitely. Initially the coil acts as a capacitor ladder network (See Fig. 7). The capacity elements are charged to nearly twice the applied E.M.F. The effective capacity being charged is. Because this network contains impedance elements of only one type the voltage distribution is hyperbolic rather than periodic. If %=distance/total length and e is voltage to ground at the particular distance, . For Tesla coils this distribution should be as linear as possible (small a). As the distribution goes from initial to final the voltage can be analyzed into a complex series of decremental waves at various frequencies and wavelengths. This is accomplished by analyzing the initial distribution (hyperbolic) into space harmonics with respect to the final (DC) distribution. If a is considerable, no linear relation exists between frequency and wave length. (See Fig. 8) When an oscillating wave follows the initial impulse (as is the FIG 7 19

K = 1 / Cs Darafs

Initial Response

Distribution along coil

Fig 8 Final Response 20 case with the Tesla transformer) the alternate positive and negative voltages cause continuous increase in voltage and energy. The effect of the alternations is to increase the amplitude of the wave by twice the applied voltage for each alternation. Example - oscillating voltage is 1.24 times applied voltage. (initial) At each cycle this is multiplied by twice Ea, causing E to ground to increase in step. At second cycle E is 4.72, at third E is 7.20, etc. This effect is reduced or suppressed by large u or a. The action of the spark gap has a multiplicative effect also. Consider Steinmetz' analysis. "Continual or cumulative oscillations involve an energy supply to the system. If the energy supply is less than energy dissipation the OSC. damps as a transient with reduced u. If the supply equals the dissipation the OSC is continuous. If supply is greater the OSC is cumulative. The OSC represent energy and frequency transformation from the L.F. or D.C. supply to the H.F. OSC system. This transfer may - be brought about by the transient of energy readjustment resulting from a change in circuit conditions, producing again a change in circuit conditions and thereby an energy adjustment by transient, etc., etc. . . Recurrent oscillations tend to run into each other and form continuous OSC. When successive transients run in to each other they tend to synch. However, the formation of continuous OSC is not the mere overlap or running together of successive waves. The recurrent OSC cannot start until the preceding OSC has died out, and sufficient charge time has elapsed for next arc over of gap. With overlap no dead period occurs during which normal or supply frequency is supplied. Energy then must be supplied by a phase displacement within arc

FIG - 9

Line elemental

    dx

During oscillation, which gives a negative energy cycle or a reversed hysteresis loop. For continuous oscillation then, a hysteresis loop must be formed by the lag of effect before cause." (This is negative resistance or the formation rather than the dissipation of energy.) "For the cumulative oscillation, the area of the loop must depend on and increase with the stored volt amps of the oscillating system." Mathematic analysis (See Fig. 9) (See reference 2) e = E to ground es = E gradient (E/inch) By Kirchoff's Law

 (23a)

Let = space operator Let = time operator Then Differentiation of (23a) in tine gives

 (23b)

These, (23a) & (23b) are independent of initial and final distribution of EMF. Equation (23b) must be expressed in one variable. In terms of voltage and current, the current density in capacity to ground is C per inch of coil times the rate of change of e to ground.

 (26)

and

 (27)

Relating Is and voltage Is in capacity between turns equals capacity per inch times the time rate of voltage gradient.

 (28)
 (29)

Relating I. and voltage: The relation between magnetizing current and I1 is complex and defies analysis. (See Fig. 10). For the fundamental distribution (1/4 wave) the effective inductance of the coil is the space integral of the 1/4 cosine wave of current of M.M.F. and is equivalent to 2/ times the normal total inductance. For the third harmonic, 3/4 cosine wave of current or M.M.F. the inductance of 1/3 of the coil opposes the remaining inductance resulting in diminishment of self induction depending on the mutual inductance of the bucking section to the rest of the coil. The process progresses similarly for the rest of the harmonic series (5F, 7F, 9F, etc.). This results in surge impedance for each harmonic but effects tend to cancel for wave length. Capacitance of the coil behaves in a similar fashion and may be voltage dependent giving the coil voltage gain under the proper conditions. (Parametric amplification) Denoting this residual inductance as leakage inductance L, and —2 —1 the dimensions of 1 as the mutual inductance M (Henry ), then

 (30a)  (30b)

FIG 10 Magnetic Distribution (30b) gives the value of , while (23a) involves . If we differentiate the former with respect to x and the latter with respect to t, substitution becomes possible.

 (31)

(31), (29) and (27) express in terms of volts the three terms of (23b) Hence, the general equations

 (33) This equation neglects losses.

Analysis of the interaction between the earth and various coils is possible by the use of velocity measure. This in general is a complex quantity consisting of real and imaginary parts. By the relation well known:

 (34)

where v is the velocity of the wave. Then velocity is the ratio of time to space. Letting this velocity be of unit value, time and space functions become equivalent, . Steinmetz gives the following instructions for accomplishing this.. "Line constants are typically given per unit length, as per centimetre, mile, 1000 feet, etc. The most convenient unit of length, when dealing with transients in distributed circuits, is the velocity unit v. That is, choosing as unit length the distance of propagation in unit time, or 3 times 1010 cm/sec for transverse waves in air, this gives v = 1 and therefore LC = 1 = C = L-1; L = C-1 That is, the capacity per unit of length, in velocity measure, is inversely proportional to the inductance. In this velocity unit of length, distance will be represented by." Substituting= 1

Time angle Distance angle Analysis of the travelling wave along Tesla coil* utilizing the light second. The equation for standing waves on a line are as follows:

 (1)

u is the power dissipation constant. The power involved is:

 (2)

Because the sineterm makes this symmetrical about zero the average power is zero. For the travelling wave:

 (3) The power involved is :
 (4)

Power average is now:

 (5)

• Steinmetz's analysis modified.

Thus two waves exist, a travelling steady power flow given by (5) and a standing wave given by (2) such a flow of power flows along the different sections of the Tesla transformer, consisting of sections of different u. For instance the primary has very low u due to the large surfaces and the negative u of the arc, the secondary has a higher u due to no arc, the Tesla coil has higher yet due to the small conductor size of winding, and the dielectric antenna has a very high u due to radiation. In the primary the duration of oscillation is very great as u is zero or negative. The duration of coil oscillation is shorter due to their higher u, and by themselves their OSC would dampen quickly. Since all are connected together, all must dampen together. It then follows that power must flow during transient from primary to antenna, so as to have all sections dampen together. Three conditions can occur in the general compound system: a) The power flow is uniform, that is, the power remains constant in the direction of propagation. b) The flow decreases in the direction of propagation. c) The flow of power increases in the direction of propagation. This last case is of special interest in the Tesla transformer as it increases the steepness of the wavefront, producing greater displacement current. If the flow of power increases along system, more power leaves every line element than enters it; that is, the line element is drained of its stored energy by the passage of the wave, and then dies down with time at a faster rate than by its own dissipation. That is, not all the stored energy of the line elements supplies the power dissipated in the line elements, but part of the energy leaves the elements in increasing the flow of power along the line. The rate of dissipation thus is increased, and instead of u, u+s enters the equation. That is the time decrement is:

s is the power transfer constant. But, inversely, along the line the power flow increases, that is, the intensity of the wave increases, by the same factor,

or rather, the wave decreases along the line at a slower rate than that scattered by the power dissipation. Therefore, that taken from the time domain is transferred to the space or distance domain.

Similar for e

The power transfer constant s determines the steepness of the wavefront. To meet these requirements the u of the line must exceed the average uo of system. Example (See Fig. 11):

Transformer Line Load Length = in light seconds 1.0x10-3 1.5x10-3 0.5x10-3 Dissipation = u 100 u 0.1 900 1.35 1600 0.8 uo= u AVG. =

 = 800

and s = +700 -100 -800 FIG 11

30 The transformer thus dissipates power at a rate u=10 0 but sends power at the rate of S=700, or seven times as much as it dissipates by internal losses. The load dissipates power at u - 1600 and receives power at the rate -S=800, that is 1/2 the power it dissipates is supplied from other sections, in this case the transformer. The transmission line dissipates power at the rate of u=900 only a little faster than the system uo of 800; and the line receives power at -S=100, that is, receives only 1/9 of its power from the transformer; the rest comes from its stored energy. For the special condition of waves increasing in magnitude towards lead;

Transformer

Line Load

 =

1x10-3

1.5x103 0.5xl0~3 u = 100

500 1600 uX= 1.0

0.75 0.8

Uo= AVG u =

= 533

S = +433 +33 -1067 That is the power transfer constant of the line has become positive S=33 and the line now assists the transformer is supplying power to the load (See Fig. 12). The preceding paper has attempted to show the considerations involved in the optimization of the Tesla transformer. The enormous number of factors involved make this a difficult task indeed! The authors of coil analysis have come up with conflicting results and an attempt towards resolve has been made. Solutions to the differential equations have not been given due to lack of generality of those available and lack of space. It has been mentioned in papers on the subject of coil oscillations that theory does not match practice. Much more experimentation is necessary. it also might be possible that does not give the proper velocity, remembering that Tesla claims that his velocities are faster than light. For further information see: 1. ABNORMAL VOLTAGES IN TRANSFORMERS. J. M. Weed. American Institute of Electrical Engineers. Sept. 1915, p.2157. 2. ABNORMAL VOLTAGES WITHIN TRANSFORMERS. L. F. Blume. Feb. 1919, American Institute of Electrical Engineers, p. 577.' 3. ELECTRIC WAVES, DISCHARGES AND IMPULSES. C. P. Steinmetz 4. TRAVELING WAVES ON TRANSMISSION SYSTEMS. Bewley, L.V. 1938, 1951. Dover. 5. DIELECTRIC PHENOMENA IN HIGH VOLTAGE CABLES. D. M. Robinson, 1936. 6. ROENTGEN RAYS AND PHENOMENA OF THE ANODE AND CATHODE. E. P. Thompson. 1896, Van Nostrand Co., p. 93 (Kelvin), p. 136 (Tesla).

— Energy Distribution in Compound Oscillation of Open Circuit. Paster Than Light! By HUGO GERNSBACK IT may com as a shock, to most students of science, to learn that there are still in the world some scientists who believe that there are speeds greater than that of light. Since the advent of Einstein, most scientists and physicists have taken it for granted that speeds greater than 186,800 miles per second are impossible in the universe. Indeed, one of the principal tenets of the relativity theory it that the mass of a body increases with its speed, and would become infinite at the veloc­ity of light. Hence, a greater velocity is impossible. Among those who deny that this is true, there is Nikola Tesla, well known for his hundreds of im­portant inventions. The induction motor and the sys­tem of distributing alternating current are but a few of his great contributions to modern science. In 1893, be made his historic experiments in Colorado; where he manufactured, for the first time, artificial lightning bolts 100 feet long, and where he was able, by means of high-frequency currents, to light electric lamps at a distance of three miles without the use of any wires whatsoever. Talking to me about these experiments recently. Dr. Tesla revealed that he had made a number of sur­prising discoveries in the high-frequency electric field and that in the course of these experiments, he had become convinced that he propagated frequencies at speeds higher than the speed of light In his patent No. 787,412. filed May 16, 1900, Tesla showed that the current of his transmitter passed over the earth's surface with a speed of 292,880 miles per second, while radio waves proceed with the velocity of light. Tesla holds, however, that our present "radio" waves are not true Hertzian waves, but really sound waves. He informs me, further, that he knows of speeds several times greater than that of light, and that he has designed apparatus with which he expects to project so-called electrons with a speed equal to twice that of light. Coming from so eminent a source, the statement should be given due consideration. After all, abstract mathematics is one thing, and actual experimentation is another. Nut so many years ago, one of the world's greatest scientists of the time proved mathematically that it is impossible to fly a heavier — than — air machine. Yet we are flying plenty of airplanes today. Tesla contradicts a part of the relativity theory emphatically, holding that mass is unalterable: other­wise, energy could be produced from nothing, since the kinetic energy required in the fall of a body would be greater than that necessary to lift it at a small velocity. It is within the bounds of possibility that Einstein's mathematics of speeds greater than light may be-wrong. Tesla has been right many times during the past, and he may be proven right in the future. In any event, the statement that there are speeds faster than light is a tremendous one, and opens up entirely new vistas to science. While it is believed by many scientists today that the force of gravitation is merely another manifesta­tion of electromagnetic waves, there have, as yet, been no proofs of this. There are, of course, many obscure things about gravitation that we have not, as yet, fathomed. At our time, it was believed by many scientists that the speed of gravitation is instantaneous throughout the universe. This is simply another way of putting it that there are speeds greater than light. Yet, from a strictly scientific viewpoint, no one to­day has any idea how fast gravitational waves—always providing that the force is in waves—travel. If the moon, for instance, were to explode at a given moment, how long would it be before the gravitational disturb­ance would be felt on earth? Would the gravitational impulse or waves travel at the speed of light—that is, 186,000 miles per second—or would the effect be in­stantaneous? We do not know. The entire subject will no doubt arouse a tremendous interest in scientific circles. It is hoped that other scientists will be encouraged to investigate Dr. Testa's far-reaching assertions; either to definitely prove or to disprove them. FIG 12 CAPACITIES* By Fritz Lowenstein As the seat of energy of an electrical field is in the space outside of the charged bodies we will consider the shape and concentration of the field only, but not that of the body itself. This distinction is necessary because capacities are usually attributed to the bodies? charged, whereas the energy is excluded from that space which is occupied by the body. Considering the space between two charged bodies as the only seat of energy, the expression "charged body" is best replaced by "terminal surface" of the field. Comparing geometrically similar elements of two geo­metrically similar fields, the elementary capacities are pro­portional to lineal dimensions. (See Figure 1.)

Extending this law over the entire field by the integrating process, we find that geometrically similar fields have capacities proportional to the lineal dimensions of the terminal surfaces. It is to be expected, therefore, that capacities expressed in dimensions of terminal surfaces should be of lineal dimensions. That the capacity is by no means a function of the volume of the field or of the terminal body may be easily seen from Figure 2 where a field element is increased to double the volume by adding

• Presented before The Institute of Radio Engineers, New York, Decem­ber 1, 1915.

17 volume in the direction of the field lines and in a direction per­pendicular to the lines. In the first case the capacity has been decreased whereas in the latter case increased, altho in both cases the volumetric increase is the same.

Figure 2 It is seen, therefore, that instead of being dependent on the volume, the capacity is rather a function of lineal dimension and therefore the maximum lineal dimension predominates. An interesting example of this predominating lineal dimension or "maximum reach" is given by the composite capacity of two wires joining at one end under various angles, as shown in Figure 3.

Figure 3 When the angle is small the composite capacity is practically the same as that of the single wire, since the addition of the second wire has not increased the maximum reach. If the second wire B be joined to A at an angle of 180 degrees, which means in straight continuation of wire .,4 the total capacity has 18 . ■ doubled, as the maximum reach now is twice that of the single wire. We notice also that by deviating wire B slightly from the straight continuation of wire A, the maximum reach of the system is not materially altered, from which one may correctly conclude that turning the wire B thru an appreciable angle b does not materially change the capacity of the system. On the other hand a great change of maximum reach is produced by variations of the angle when the two wires are approximately perpendicular, and in fact the en parity of the total structure is most sensitive to changes of angle between the two elements at about 90 degrees. In Figure 4, I have given a table of capacities per centimeter of the greater lineal dimension of the different configurations.

In Figure 5 the wire A B is assumed to be moved by the variable abscissae x, thereby generating a conducting sheet S. It is instructive to follow the variation of the capacity Cx. 19 At the capacity is that of the wire Cab; as long as x is small the capacity is practically constant because the width of the sheet is small compared to the length A B and a change of x does not involve a change of the predominating lineal dimension; however, as x increases and finally becomes greater than AB, it assumes the part of the predominating dimension, and, indeed, the graph shows the capacity then to be propor­tional to x.

Comparing the capacities of a sphere and of a wire, it is found that the capacity of the sphere is only three or four times as great as the capacity of the wire in spite of the million times greater volume. I have spoken of the capacities of a wire and of other bodies instead of the capacity of the field simply because I do not wish to distract attention from the familiar conceptions. Let me analyze the field shown in Figure 6, having two concentric spheres as terminal surfaces, and defining as "volumetric energy density" the energy contained in one cubic centimeter. As the energy of a field element is made up of the product of potential along the lines of force within that element and of the number of lines traversing it. the energy of a cubic centimeter of electric field is proportional to the square of the field density. "Since the field density diminishes as the square of the distance from the center of field, the volumetric energy density diminishes with the fourth power of the distance from the center. The diagram to the left in Figure 6 shows the decrease of volumetric energy density. . . Of greater interest than the volumetric energy density is the lineal energy density, which may be defined as the energy contained 20

in a spherical layer of one centimeter radial thickness: and as the volume of such layer increases with the square of the distance from the center, the law follows from this fact, and from the volumetric energy density law that the lineal enemy density decreases inversely as the square of the distance from the center. Such dependence is graphically shown to the right in Figure 6. The shaded surface below this curve represents the total energy of the field and it is easily seen therefrom that the maximum energy of the field is concentrated near the smaller of the two spheres. I have taken a simple case of a field with spherical terminal surfaces to show that the concentration of energy lies near the smaller terminal surface. Similar considerations can he applied when substituting for this field radiating three-dimensionally. a field of bi-dimensional radiation (as that occurring in the case of long cylindrical terminal surfaces): where, as in this instance. the bulk of the energy of the field is to be found near the smaller ore of the two terminal surfaces. In Figure 7. I have shown a field with concentric terminal surfaces (either spherical or cylindrical), and have increased the scope of the field by reducing the size of the smaller terminal surface without, however, changing either the total number of field lines or the larger terminal surface. As the lineal energy density is very great near the smaller terminal surface, such addition of the field at that point must have materially increased the energy of the field and the change in capacity to be expected should be considerable. In fact, a considerable change in capacity of a sphere is obtained by a change of its diameter. If. in Figure 7 the larger terminal surface alone is changed, 21 even materially, the total energy of the field will be increased very slightly only; due to the fact, as we have seen, that the energy density near the larger terminal surface is very small. Such a small change in energy- corresponds to only a small change in the capacity of the field, from which we conclude:

In .1 field having two terminal surfaces of greatly different size, a change of the smaller surface produces a great change in capacity, whereas a change of the larger terminal surface affects the capacity of the field only very slightly. The capacity of a field is, therefore, almost entirely determined by the shape of the smaller terminal surface. That is why we may with correctness speak of the capacity of a sphere, or any other body, without mentioning the size and shape of the other terminal surface, as long as the assumption is correct that such other terminal surface is of greatly larger dimensions. It may not l>e amiss to call your attention to the fact that the increase of field energy as illustrated in Figure 7 is accom­panied by a decrease in capacity. This relation may easily be deduced from physical considerations, as well as. from con­sideration of the mathematical expression for the capacity

wherein the capacity is expressed as a property of the field alone. I am tempted to introduce here the reciprocal value of capacity and apply to it the term "'stiffness of the field," as an increase of energy would he followed by an increase of stiffness. I am, 22 however, loath to mar any additional insight which may be gained from these explanations by deviation from so familiar a term as capacity. For a better conception of the slight change of capacity caused by a considerable increase of the larger terminal surface, I refer to Figure 7, where the difference of capacity is only 1 per cent in spite of the diameter of the larger terminal surface being increased 100 per cent. It appears, therefore, that that part of the capacity of an antenna which is due to the flat top is not materially changed by its height above ground. While considering the capacity of a flat top antenna to ground, it must have occurred to many engineers, as it did to me, that the statement to be found in many text books on electro­statics is rather misleading: "That the free capacity of a body considered alone in space must not be confounded with the capacity the body may have against another body considered as a plate condenser." This statement is quite erroneous. As the strength and direction in any point of a field is of single and definite value, only one electric field can exist in a given space at a given moment, and, therefore, only one value of capacity. It is incorrect, therefore, to distinguish between free capacity and condenser capacity. This clarifying statement is deemed advisable, or at least permissible, in view of the quoted errors. By speaking of the capacity of the field instead of that of the body, no such erroneous thought is possible, and it is clear that by free capacity of a body is meant the capacity of the field whose smaller terminal surface is the given body and whose larger terminal surface is one of vastly greater dimensions. It is not essential that this greater terminal surface be located at infinite distance, because of the fact that even if construed as of ten times the lineal dimensions of the small surface the change caused by removing it to an infinite distance would result in a change in capacity of not more than one-tenth of 1 per cent. At a time when I had not realized the singly determined value of a field capacity, I considered a comparison between free and plate capacity as shown in Figure 8, wherein to an upper

disc (of which the free capacity is (2/PI)*r). was added another lower disc, thereby forming a plate condenser. The problem arose in rny mind to determine the distance of separation of the two plates so that the plate capacity would equal the free capacity of the single disc. From the well-known formulas for the disc 23

Figure 8 capacity and plate capacity, it would appear that the two were equal at a distance equal to d= (PI/8)r, and I must confess that I had quite a struggle to decide whether in speaking of the capacity of the upper plate I would not have to add the two capacities. While such a mistake need hardly be called to the attention of the majority of engineers, I do not hesitate to make mention of it for the benefit of even the few students who might gain therefrom. The advent of the aeroplane has opened another field, for radio communication. Whereas in the static field of an antenna, one terminal surface is artificial and the other provided by the surrounding ground, both terminal surfaces in an aeroplane outfit have to be artificial and are, therefore, open to design. The question arises in such a radio oscillator as to how much may be gained in energy for each single charge by increasing that one of the two terminal surfaces which consists of a dropped wire. The arrangement is shown in Figure 9. It is evident that Figure 9 24

as long as the dropped wire is of smaller dimensions than the electrostatic counterpoise provided on the aeroplane, an increase in length of such dropped wire will materially increase the capacity of the field and, therefore, the energy per charge (as we may conclude by analogy from Figure 7). As soon, however, as the dropped wire is materially longer than the conductor on the aeroplane it assumes the role of the larger terminal surface of the field, and any further increase of its length will not materially contribute to an increase of electrostatic capacity nor of the energy per unit charge. Figure 10 shows the function of the volumetric and lineal energy density in a field whose smaller terminal surface is a long cylinder. Such a field, radiating bi-dimensionally only, shows an energy concentration not so accentuated as that found in the

Figure 10 tri-dimensionally radiating field; but considering the larger terminal surface of a diameter ten times that of the smaller surface, the capacity would only be changed 1 per cent by increasing the larger terminal surface infinitely. In all cases, therefore, where the larger terminal surface does not come closer at any point than (say) ten times the corresponding dimension of the smaller terminal surface, we need not be concerned with the actual shape of the larger terminal surface when we determine the seat of energy, the capacity and the configuration of the field lines emanating from the smaller surface. It will be seen, therefore, that from the flat top of an antenna, lines emanate almost symmetrically both upwards and. downwards as though the larger terminal surface were one 25 surrounding the antenna symmetrically on all sides, in spite of the fact that the ground is located entirely at the bottom of the antenna. This is clearly illustrated in Figure 11. By integrating the lineal energy density of a three-dimen-sionally radiating field between the radius of the smaller sphere

Figure 11

Mr. Nikola Tesla, and ( expect to come back to the behavior of a sphere as a conductor of radio frequency currents at some later date. The study of capacities of composite bodies is most in­structive and conducive to a clear conception of capacity. Let. as in Figure 13. a number of small spheres of radius be so arranged as to cover completely the surface of the larger sphere, the radius R of which be 100. If each one of the

31,400 smaller spheres could be counted at its full value of capacity, the capacity of the composite body would be 31,400; as a matter of fact, however, it is not more than radius R of the larger sphere, that is 100. Indeed, the configuration of the electric field F could not have changed materially by the arrangement of the small spheres, and the capacity clearly presents itself as a property of the configuration of the field lying outside of the enveloping surface of the composite structure. 27 Capacity may play a part in the conduction of electricity thru liquids and gases. Let us assume a series of spheres in lineal arrangement as shown on Figure 14. As long as the distance between the spheres is great com­pared to the diameter of the spheres, each sphere will retain its full capacity as given by its radius. By decreasing the distance

between spheres the individual capacities of the spheres decrease, because of the negative capacity coefficients. If such approxima­tion be carried to the point of contact between the spheres, the capacity of each individual sphere would be reduced to ap­proximately - of the original capacity. If such a row of spheres were conceived as freely movable, so as to enable each sphere to make contact with a plate P, which is kept charged to a certain potential, then the charges carried away by the spheres after contact with the plate would be proportional to the full capacity of each sphere as long as the spheres are far apart, and would bo only 1/s = 1/2.718 th part of such maximum charge when the spheres are in contact. As we assumed the plate P to be main­tained at a certain potential by an outside source of electricity, the convention current represented by the departing charges of the spheres would vary approximately in a ratio, of 2.71 to 1. In the passage of electricity thru an electrolyte, the molecular conductivity has been found to be the same for all electrolytes, and varying only with the concentration of the solution; the molecular conductivity being approximately 2.5 times as great in the very dilute solution as in the concentrated solution. I wish to call your attention to the striking similarity between the ratio of conductivity experimentally determined in elec-

                                   .

trolytes of small and large concentration and the ratio of con­ductivity of the row of spheres where the spheres are far apart or close together. I do not pretend at this moment that a

plausible modification of the theory of conduction thru elec­trolytes and gases can be bused on such a coincidence; and in fact, assumptions would have to be made. For example, a lineal arrangement of the ions in the direction of the static field impressed on the electrolyte or on the gas must be assumed.

But the fact that such ratio in the case of the spheres is deduced from geometrical considerations alone, coupled with the fact that in electrolytes the same ratio follows from purely geometrical considerations, is sufficient to warrant further thought. I do not hesitate to bring this interesting coincidence to your knowledge, with the hope that other physicists may carry on investigations in the same direction. I have said that the molecular con­ductivity of electrolytes arose from geometrical considerations only, and I think it advisable to call your attention to the founda­tion of such a statement. While it is true that the conductivity of different electrolytes varies considerably, it has been found that the molecular conductivity is the same for all electrolytes. The similar behavior, of the same number of molecules, in­dependently of the weight of the molecule, therefore reduces the phenomenon to a purely geometric basis. SUMMARY: Considering that electrostatic energy is actually in the space surrounding a charged body, the Utter is called a "terminal surface." It is shown that capacity is predominantly a function of the maximum lineal dimension of the terminal surface. The volumetric and lineal energy den­sities in the field are defined and studied in a number of cases. It is proven that the capacity between two terminal surfaces is greatly affected by chang­ing the lineal dimensions of the smaller terminal surface, but not so for changes of the larger. Certain current errors in connection with "mutual capacity" are considered. The practical applications to a radio antenna and to aeroplane counter­poises arc given. When a charge traverses a sphere, entering parallel to a diameter, the sphere behaves as a conductor of uniform lineal capacity. Applications of the theoretical considerations are also given in connec­tion with the conductivity of concentrated and dilute electrolytes.