Fast Light

Interessant detail is dat E = n m v^2 = M v^2 er uit komt. Dan is het weer verwarrend dat het hier om maessa en niet om massa zou gaan. Hoewel, het verklaard misschien ook meteen weer iets. "Another interesting observation is that in this model which is founded upon Maxwell’s, charge itself is a basic oscillation of momentum at each and every point in the field and with units of kg/sec we finally realize that the charge to mass ratio is simply the oscillation's frequency $\nu$".

$\nu$ = de frequentie van een "foton".

Dus als je een vortex hebt, die f keer per seconde roteert..

Dan krijgt zo'n ding een lading q.

En dan geldt: q = f * m

En aangezien de ruimte vol zit met EM trillingen, heb je dus in feite een ruimte, die over de gehele ruimte bezien een gedistribueerde lading bevat, die uitgedrukt kan worden in ladingsdichtheid. En ladingsdichtheid is dan weer de tijdsafgeleide van m. Eigenlijk kun je dus stellen:

"achtergrondstraling" == "gedistribueerde lading" == maessa in beweging.

En zwaartekracht is dan weer de afgeleide van E, het electrisch veld.

Die is 1 / (4 pi eps_0) q/r*r

q invullen

E = 1 / (4 pi eps_0) f*m/r*r

Enige groothed die gedifferentieerd kunnen worden naar locatie, zijn m en r. Bij differentieren krijg je dus een veld dat afhankelijk is van m, r en r^2, beschreven door een 2e graads functie. Ofwel: zwaartekracht is de tweede afgeleide van een functie van f en m. En als het gaat om *harmonische* bewegingen, al dan niet in werkelijkheid roterend, dan zijn de afgeleiden van een functie ook *harmonisch* met dezelfde frequentie.

Of *harmonischen* daarvan Dus de golven die ontstaan, zijn per definitie in fase, aangezien oorzaak + gevolg veroorzaakt worden door 1 en dezelfde lokale trilling. De voortplantingssnelheid van zwaartekracht is dus per definitie gelijk aan die van het dielectrische E veld. Het interessante is nu dat objecten eigenlijk altijd naar beneden vallen, ofwel naar moeder aarde toe. En we hebben drie domeinen: drie behoudswetten (maessa, eimpuls, eneregie), drie dimensies. Aangezien het ding naar beneden valt, gaan we er vanuit dat moeder aarde de energie levert om het ding te laten vallen. Er is dus een dielectrische / zwaartekracht golf, waarbij de "voedende" energie vanuit de aarde komt.

Een Einsteiniaan zou nu roepen: "Oh jee, mijn golf gaat terug in de tijd!!" 😀

Nee, dus. Er zijn interessante experimenten gedaan met "fast light" http://www.tuks.nl/pdf/Reference_Material/Fast_Light/

Ik dacht aan Stenner:

http://www.tuks.nl/pdf/Reference_Material/Fast_Light/Stenner%20-%20The%20speed%20of%20information%20in%20a%20fast-light%20optical%20medium.pdf

The possibility of superluminal group velocities (vg > c or vg < 0) was such a concern to researchers around 1910 that several conference sessions were devoted to the topic. Based on these discussions, Sommerfeld demonstrated theoretically that the velocity of the front of a square-shaped pulse propagating through any medium is identically equal to c and hence relativistic causality is preserved. In a follow-up study, Brillouin suggested that the group velocity is not physically meaningful when the dispersion is anomalous because the pulse becomes severely distorted. More recent research investigating the propagation of smooth-shaped pulses has shown that this conclusion is not justified, leading to renewed controversy.
Another outcome of the discussions in the early 1900s, as recounted in the preface and first chapter of the book by Brillouin, was a reformulation of the fundamental postulate of the special theory of relativity. This reformulation states that, rather than limiting the speed of an ‘object’, it is the information velocity vi that is limited by c. Unfortunately, there is no agreed-upon definition of the information velocity.
In our experiment, we use a fast-light medium that exploits the spectral region of anomalous dispersion between two closely spaced amplifying resonances realized by creating large atomic coherence in a laser-driven potassium vapour, as shown in Fig. 1a. We obtain larger pulse advancement for a smooth gaussian-shaped pulse, as shown in Fig. 1b, in comparison to the experiment of ref. 15, by increasing the gain and hence the size of the anomalous dispersion. The larger advancement relative to the pulse width obtained in our experiment makes it easier to distinguish the different velocities describing pulse propagation. From this data, we infer that ng = -19.6 +/- 0.8, indicating that we are operating in the highly superluminal regime.
Figure 1 Fast-light pulse propagation.
a, Experimental set-up. The potassium vapours are contained in two uncoated Pyrex cells of length L /2 = 20 cm (to suppress unwanted parametric instabilities) and heated to obtain an atomic number density of 4.5 x 10 11 atoms cm-3. Linearly polarized coherence-preparation laser beams (frequencies $\omega_{d+}$ and $\omega_{d-}$) are combined with the linear and orthogonally polarized pulses using polarizing beam splitters. The pulses are detected by a photoreceiver with a 25 kHz–125 MHz bandwidth. The coherence preparation beams are adjusted with $\omega_{d-}$ set at 1.36 GHz to the high-frequency side of the centre of the potassium 4S1/2 <-> 4P1/2 transition and $\omega_{d+}$ - $\omega_{d-}$ = 23 MHz, chosen to optimize the pulse advancement using procedures similar to those discussed in refs 15, 18 and 22. The pulses are generated by passing a continuous-wave laser beam through an acousto-optic modulator (AOM) driven by a computer-controlled arbitrary waveform generator. The time origin has been set arbitrarily to coincide with the peak of this pulse.
b, The solid line shows the temporal evolution of a 263.4-ns-long (full-width at half-maximum) pulse propagating through the cells when the lasers are tuned far from the atomic resonance and hence the vapour-cell portion of the path is equivalent to vacuum. The dashed line shows the observed fast-light pulse advancement for a smooth pulse shape when the coherence-preparation laser is tuned near the atomic resonance and q o is set between the gain resonances. The peak of the pulse is advanced by t adv 1⁄4 27.4 ns ^ 1.1 ns, corresponding to a relative pulse advancement of 10.4%. Using t adv 1⁄4 L /c 2 L /v g with L /c 1⁄4 1.3 ns, we find v g /c 1⁄4 20.051 ^ 0.002. Careful inspection of the fast-light pulse reveals that it has been compressed by 1.9%, which is due primarily to the frequency dependence of the gain.

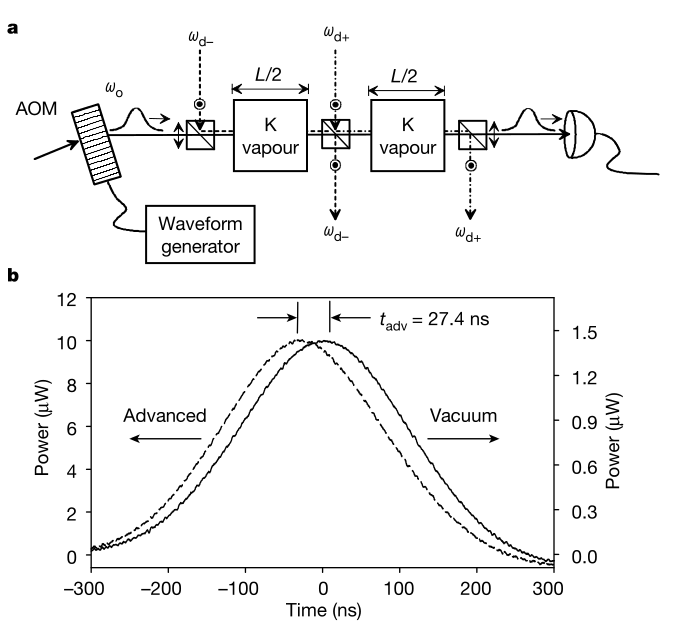
So, the advancement (27 ns) is much bigger than the time the wave is supposed to spend in the gas region (1.3 ns). Compare this with the findings of Wang et al:

However, in all previous experimental demonstrations, the light pulses experienced either very large absorption or severe reshaping, resulting in controversies over the interpretation. Here we use gain-assisted linear anomalous dispersion to demonstrate superluminal light propagation in atomic caesium gas. The group velocity of a laser pulse in this region exceeds c and can even become negative, while the shape of the pulse is preserved. We measure a group-velocity index of ng = -310 (+/- 5); in practice, this means that a light pulse propagating through the atomic vapour cell appears at the exit side so much earlier than if it had propagated the same distance in a vacuum that the peak of the pulse appears to leave the cell before entering it.
The observed superluminal light pulse propagation is not at odds with causality, being a direct consequence of classical interference between its different frequency components in an anomalous dispersion region.

If indeed the observed propagation speed is that much greater than the speed of light that the "superlimunal light pulse" appears to leave the cell before entering it, it is hard to conclude otherwise than that the "anomalous dispersion region" is not confined to the region filled with gas, but extends beyond that region, such that the anomalous process takes (much) larger part of the total signal path than is being expected.

We can make the following estimation, assuming Paul Stowe is correct and the propagation speed of longitudinal waves is sqrt(3), or about 1.73, times the propagation speed of transverse waves. From that assumption, we can compute L/c for a longitudinal wave by computing L/(sqrt(3) c), which computes to about 0.77 ns. So, we would expect an advancement of about 0.56 ns for L=0.4 m.

Given that the measured advancement is about 27.4 ns, we can deduce the extended region wherein the anomalous dispersion takes place has a total path length LL of about 27.4/0.56*0.4 = about 19.44 m, which is unexpectedly large, although it would be possible, given that we have no information about the lengths of the various parts of the experimental setup, except for the length of the Pyrex cells.

However, the assumption of there being a difference in propagation speed of about sqrt(3) is based on the assumption that the medium is isotropic. In our model, wherein we consider far field manifestations of EM radiation to consist of a number of vortices, whereby the rotating matter is forced towards the outer region of the vortices because of centrifugal forces, we can deduce the central area of the vortices to have a significantly lower density than what our assumption is based on. This would result in a longitudinal propagation speed which is significantly less, assuming the longitudinal wave propagates trough the central low-density "hole" along the central axis of the vortex.

To summarize: our model predicts the region wherein the "anomalous dispersion" occurs to extend beyond the Pyrex cells, possibly all the way up to, for example, the polarizing beam splitters or perhaps even the resonators within the linearly polarized lasers being used. Futher, our model predicts that the propagation speed of the "fast light" may depend on the density of the medium along the central axis of the propagation path. Therefore, further experiments involving variation of the placement of the various parts of the setup could very well lead to further insights into this phenomenon.

And if our prediction of the "anomalous" region extending beyond the Pyrex cells is true and the phenomenon indeed involves the creation and propagation of a longitudinal wave, which is created as a "beat" signal with the heterodyning of two EM signals, then it is clear that longitudinal dielectric waves do exist amd that they can also propagate trough a region void of "free charge carriers", such as an optic fiber cable, air and even the vacuum.

Ok, er lijkt dus een golf te zijn, die op ons toe komt, gewoon met de tijd mee gerekend, natuurlijk.

En aangezien het ding dus recht naar beneden valt, is er geen rotatie, hoewel rotatie (van een object) wel de zwaartekracht kan beinvloeden.

Dus een dielectrische golf.

Dus een longitudinale golf.

Fast light phenomena and Lines (Tubes) of Force

One of the most interesting phenomena regarding wave propagation and the speed of light is the so-called anomalous dispersion, an anomaly which deserves our attention. On the WikiPedia page about optical dispersion we read:

The group velocity vg is often thought of as the velocity at which energy or information is conveyed along the wave. In most cases this is true, and the group velocity can be thought of as the signal velocity of the waveform. In some unusual circumstances, called cases of anomalous dispersion, the rate of change of the index of refraction with respect to the wavelength changes sign, in which case it is possible for the group velocity to exceed the speed of light (vg > c). Anomalous dispersion occurs, for instance, where the wavelength of the light is close to an absorption resonance of the medium. When the dispersion is anomalous, however, group velocity is no longer an indicator of signal velocity. Instead, a signal travels at the speed of the wavefront, which is c irrespective of the index of refraction.
Recently, it has become possible to create gases in which the group velocity is not only larger than the speed of light, but even negative. In these cases, a pulse can appear to exit a medium before it enters. Even in these cases, however, a signal travels at, or less than, the speed of light, as demonstrated by Stenner, et al.

Let us first note that:

  • neither the anomalous dispersion phenomenon itself nor the resulting phenomenon of faster-than-light wave propagation are disputed;
  • in the interpretation of the faster-than-light wave propagation, there are perceived issues with causality and for some reason a distinction is made between a "pulse" and a "signal".

So, while the existence of the faster-than-light phenomenon itself is pretty much an accepted fact, the interpretation thereof leads to confusing and contradicting statements and conclusions, as we shall see.

Now let us consider what is meant by a "pulse" and a "signal" in this context, and consider how this perceived difference led to the conclusion that while the pulse carrying the information, propagates at a speed exceeding the speed of light, the "signal", the information, nonetheless is perceived to propagate at the speed of light, c. We shall begin by considering why the assumption of an "invariant" speed of light, "the parameter c", "is ubiquitous in modern physics".

It is namely exactly this "invariant c" assumption and it's role in interpretation issues, which beautifully illustrate the ongoing conundrum coming forth from the implications thereof. It is this fundamental assumption, demanded by the Lorentz transform, and the subsequent introduction of the "curved space" concept, which led to a distorted interpretation of the "spacetime" continuum. These consequences are perhaps most notable in the interpretation of "causality" or "relativistic causality", since that leads to "paradoxes", as described by Stenner et al:

One consequence of the special theory of relativity is that no signal can cause an effect outside the source light cone, the space-time surface on which light rays emanate from the source. Violation of this principle of relativistic causality leads to paradoxes, such as that of an effect preceding its cause. Recent experiments on optical pulse propagation in so-called ‘fast-light’ media — which are characterized by a wave group velocity vg exceeding the vacuum speed of light c or taking on negative values — have led to renewed debate about the definition of the information velocity vi. One view is that vi = vg, which would violate causality, while another is that vi = c in all situations, which would preserve causality.

To explore this conundrum further, let us consider the fundamental role the universally fixed, or "invariant", speed of light c plays in the special theory of relativity:

The speed at which light waves propagate in vacuum is independent both of the motion of the wave source and of the inertial frame of reference of the observer. This invariance of the speed of light was postulated by Einstein in 1905, after being motivated by Maxwell's theory of electromagnetism and the lack of evidence for the luminiferous aether; it has since been consistently confirmed by many experiments.

Let us first note that "absence of evidence is not [the same as] evidence of absence":

In 1992 during a presentation at Caltech, skeptic James Randi said "you can't prove a negative". He claims that he cannot prove a negative (such as that telepathy does not exist), but he argues that an individual who claims telepathy exists must prove it. He contends that induction is often used as a mode of proving a thesis, but if an individual assumes that something is or is not, then the person must prove so. Further, he says, he does not take an advocacy position, as a lawyer would. He says that he cannot prove that a negative is true, but he could attempt to use evidence and induction to support a claim that he is biased toward, such as a claim that something does not exist.
Philosopher Steven Hales argues that typically one can logically be as confident with the negation of an affirmation. Hales says that if one's standards of certainty leads them to say "there is never 'proof' of non-existence", then they must also say that "there is never 'proof' of existence either". Hales argues that there are many cases where we may be able to prove something does not exist with as much certainty as proving something does exist.

This connects directly to "falsifiability" or "testability" criterion for a scientific theory:

The strength of a scientific theory is related to the diversity of phenomena it can explain, and to its elegance and simplicity (see Occam's razor). As additional scientific evidence is gathered, a scientific theory may be rejected or modified if it does not fit the new empirical findings; in such circumstances, a more accurate theory is then desired.
Scientific theories are testable and make falsifiable predictions. They describe the causal elements responsible for a particular natural phenomenon, and are used to explain and predict aspects of the physical universe or specific areas of inquiry (e.g., electricity, chemistry, astronomy). Scientists use theories as a foundation to gain further scientific knowledge, as well as to accomplish goals such as inventing technology or curing disease.

[...]

Popper summarized these statements by saying that the central criterion of the scientific status of a theory is its "falsifiability, or refutability, or testability". Echoing this, Stephen Hawking states, "A theory is a good theory if it satisfies two requirements: It must accurately describe a large class of observations on the basis of a model that contains only a few arbitrary elements, and it must make definite predictions about the results of future observations." He also discusses the "unprovable but falsifiable" nature of theories, which is a necessary consequence of inductive logic, and that "you can disprove a theory by finding even a single observation that disagrees with the predictions of the theory".

Within this context, we note:

  • The theory of the "luminiferous aether", as it was formulated at the end of the 19th and the beginning of the 20th century, lacked supportive evidence as well as failed to predict a number of phenomena that were not only predicted by the special relativity theory but were also experimentally verified;
  • the fundamental assumption upon which the special relativity theory is founded, being that the speed of light c is universally fixed c.q. constant c.q. invariant, leads to paradoxes in the interpretation of "fast-light" phenomena;
  • the fundamental assumption upon which the aether theory which failed to predict the mentioned phenomena was founded is that the aether behaves like an incompressible fluid;
  • Paul Stowe's theory, wherein this fundamental assumption of an incompressible aether is replaced by a compressible aether, predicts both the phenomena predicted by the special relativity theory as well as Quantum Mechanics, yet does not lead to the paradoxes brought forth by both of these theories.

New let us continue reading on the fundamental role the universally fixed, or "invariant", speed of light c plays in the special theory of relativity:

It is only possible to verify experimentally that the two-way speed of light (for example, from a source to a mirror and back again) is frame-independent, because it is impossible to measure the one-way speed of light (for example, from a source to a distant detector) without some convention as to how clocks at the source and at the detector should be synchronized. However, by adopting Einstein synchronization for the clocks, the one-way speed of light becomes equal to the two-way speed of light by definition. The special theory of relativity explores the consequences of this invariance of c with the assumption that the laws of physics are the same in all inertial frames of reference. One consequence is that c is the speed at which all massless particles and waves, including light, must travel in vacuum.
Special relativity has many counterintuitive and experimentally verified implications. These include the equivalence of mass and energy (E = mc2), length contraction (moving objects shorten), and time dilation (moving clocks run more slowly). The factor γ by which lengths contract and times dilate is known as the Lorentz factor.

[...]

The results of special relativity can be summarized by treating space and time as a unified structure known as spacetime (with c relating the units of space and time), and requiring that physical theories satisfy a special symmetry called Lorentz invariance, whose mathematical formulation contains the parameter c. Lorentz invariance is an almost universal assumption for modern physical theories, such as quantum electrodynamics, quantum chromodynamics, the Standard Model of particle physics, and general relativity. As such, the parameter c is ubiquitous in modern physics, appearing in many contexts that are unrelated to light.

[...]

It is generally assumed that fundamental constants such as c have the same value throughout spacetime, meaning that they do not depend on location and do not vary with time. However, it has been suggested in various theories that the speed of light may have changed over time. No conclusive evidence for such changes has been found, but they remain the subject of ongoing research.

In an article about Thévenaz's findings on science blog (still accessible via archive.org), we read:

The telecommunications industry transmits vast quantities of data via fiber optics. Light signals race down the information superhighway at about 186,000 miles per second. But information cannot be processed at this speed, because with current technology light signals cannot be stored, routed or processed without first being transformed into electrical signals, which work much more slowly. If the light signal could be controlled by light, it would be possible to route and process optical data without the costly electrical conversion, opening up the possibility of processing information at the speed of light.
This is exactly what the EPFL team has demonstrated. Using their Stimulated Brillouin Scattering (SBS) method, the group was able to slow a light signal down by a factor of 3.6, creating a sort of temporary "optical memory." They were also able to create extreme conditions in which the light signal travelled faster than 300 million meters a second. And even though this seems to violate all sorts of cherished physical assumptions, Einstein needn’t move over – relativity isn’t called into question, because only a portion of the signal is affected.
Slowing down light is considered to be a critical step in our ability to process information optically. The US Defense Advanced Research Projects Agency (DARPA) considers it so important that it has been funnelling millions of dollars into projects such as "Applications of Slow Light in Optical Fibers" and research on all-optical routers. To succeed commercially, a device that slows down light must be able to work across a range of wavelengths, be capable of working at high bit-rates and be reasonably compact and inexpensive.

Juist. Niets aan de hand. Nothing to see here. Slechts een gedeelte van het signaal gaat sneller dan c. Maar welk gedeelte dan?

"To succeed commercially, a device that slows down light must be able to work across a range of wavelengths, be capable of working at high bit-rates and be reasonably compact and inexpensive."

Juist. Het gaat om een gedeelte van het signaal, waarbij er sprake is van een beperkte bandbreedte waarbinnen sneller dan licht propagatie mogelijk is.

Wikipedia nog eens:

Anomalous dispersion occurs, for instance, where the wavelength of the light is close to an absorption resonance of the medium. When the dispersion is anomalous, however, group velocity is no longer an indicator of signal velocity. Instead, a signal travels at the speed of the wavefront, which is c irrespective of the index of refraction.

Dat is interessant. Er is dus een specifieke, medium afhankelijke, resonantie frequentie waarbij sneller dan licht propagatie optreedt, precies zoals ik betoogd heb dat dit ook in het RF geval optreedt bij antennes.

En wat ik daar ook bij betoogd heb, is dat het erg lastig is om longitudinale golven te meten. En dat is ook precies waar men hier tegen aan loopt:

Scienceblog:

Light signals race down the information superhighway at about 186,000 miles per second. But information cannot be processed at this speed, because with current technology light signals cannot be stored, routed or processed without first being transformed into electrical signals, which work much more slowly.

Although both propagate at the exact same speed, the speed of light. ^_^

The blue dot moves at the speed of the ripples, the phase velocity; the green dot moves with the speed of the envelope, the group velocity; and the red dot moves with the speed of the foremost part of the pulse, the front velocity.

http://www.tuks.nl/pdf/Reference_Material/Fast_Light/Wang%20et%20al%20-%20Gain-assisted%20superluminal%20light%20propagation.pdf

Gain-assisted superluminal light propagation L. J. Wang, A. Kuzmich & A. Dogariu

Einstein's theory of special relativity and the principle of causality imply that the speed of any moving object cannot exceed that of light in a vacuum (c). Nevertheless, there exist various proposals for observing faster-than-c propagation of light pulses, using anomalous dispersion near an absorption line, nonlinear and linear gain lines, or tunnelling barriers.
However, in all previous experimental demonstrations, the light pulses experienced either very large absorption or severe reshaping, resulting in controversies over the interpretation. Here we use gain-assisted linear anomalous dispersion to demonstrate superluminal light propagation in atomic caesium gas. The group velocity of a laser pulse in this region exceeds c and can even become negative, while the shape of the pulse is preserved. We measure a group-velocity index of ng = -310 (+/- 5); in practice, this means that a light pulse propagating through the atomic vapour cell appears at the exit side so much earlier than if it had propagated the same distance in a vacuum that the peak of the pulse appears to leave the cell before entering it.
The observed superluminal light pulse propagation is not at odds with causality, being a direct consequence of classical interference between its different frequency components in an anomalous dispersion region.

http://www.tuks.nl/pdf/Reference_Material/Fast_Light/Gonzalez-Herraez%20et%20al%20-%20Optically%20controlled%20slow%20and%20fast%20light%20in%20optical%20fibers%20using%20stimulated%20Brillouin%20scattering%20-%202005.pdf

http://www.tuks.nl/pdf/Reference_Material/Fast_Light/Thevenaz%20-%20Achievements%20in%20Slow%20and%20Fast%20Light%20in%20Optical%20Fibres%20-%202008.pdf

https://www.researchgate.net/publication/4361452_Achievements_in_slow_and_fast_light_in_optical_fibres

Ze hebben het over acoustische golven

Maar: "This stimulation is efficient only if the two optical waves show a frequency difference giving a beating interference resonant with an acoustic wave (that is actually never directly observed)."

Ofwel: acoustische golven die niet daadwerkelijk "direct" waargenomen kunnen worden.

Oh, dan.

Dan zullen het wel "virtuele acoustische golven zijn". Golven die je niet kunt waarnemen, maar er wel moeten zijn, anders klopt ons verhaaltjje niet. zucht.

Hoezo, "longitudinale golven zijn nooit aangetoond"?

Men legt hier overigens wel heel mooi het principe uit van hoe twee - in verschillende richtingen propagerende - EM golven geassocieerd worden met scal^H^H^H^H acoustische golven. 😀

Je hebt bij deze "anomaliteit"dus een glas vezel

Een glasvezel fiber, door twee EM, dus roterende golven, tegen elkaar in bewegen. De roatie-richting van beide golven is echter gelijk.

Normaal gesproken krijg je zoiets als je de fiber afsluit met een spiegeltje, waardoor er een staande golf onstaat, doordat de ingaande golf reflecteert op de spiegel.

Wat ze nu doen is niet een spiegeltje op het eind, maar een "pump" golf. En de frequentie daarvan wijkt een klein beetje af dan de frequentie van het signaal dat ze op de ingang zetten.

Dus je krijgt een "beat", een verschil frequentie.

En je krijgt dus een longitudinale golf op die "beat frequentie", die in de buurt moet liggen van een "absorptiefrequentie" van het medium.

Zoals bijvoorbeeld de 21 cm "waterstoflijn" op 1400 MHz.

https://en.wikipedia.org/wiki/Hydrogen_line

The hydrogen line, 21-centimeter line or H I line[1] refers to the electromagnetic radiation spectral line that is created by a change in the energy state of neutral hydrogen atoms. This electromagnetic radiation is at the precise frequency of 1420.405751786 MHz,[2] which is equivalent to the vacuum wavelength of 21.10611405413 cm in free space. This wavelength falls within the microwave radio region of the electromagnetic spectrum, and it is observed frequently in radio astronomy, since those radio waves can penetrate the large clouds of interstellar cosmic dust that are opaque to visible light.
The microwaves of the hydrogen line come from the atomic transition of an electron between the two hyperfine levels of the hydrogen 1s ground state that have an energy difference of 5.87433 µeV.[3] It is called the spin-flip transition. The frequency, ν, of the quanta that are emitted by this transition between two different energy levels is given by the Planck–Einstein relation E = hν. The constant of proportionality, h, is known as the Planck constant.

https://en.wikipedia.org/wiki/Planck%E2%80%93Einstein_relation

The Planck–Einstein relation[1][2][3] is also referred to as the Einstein relation,[1][4][5] Planck's energy–frequency relation,[6] the Planck relation,[7] and the Planck equation.[8] Also the eponym 'Planck formula'[9] belongs on this list, but also often refers instead to Planck's law[10][11] These various eponyms are far from standard; they are used only sporadically, neither regularly nor very widely. They refer to a formula integral to quantum mechanics, which states that the energy of a photon, E, is proportional to its frequency, ν: 

    $ E=h\nu $

The constant of proportionality, h, is known as the Planck constant. Several equivalent forms of the relation exist.

The relation accounts for quantized nature of light, and plays a key role in understanding phenomena such as the photoelectric effect, and Planck's law of black body radiation. See also the Planck postulate.

Dit is een paper van Thévenaz dat wellicht meer details geeft:

http://infoscience.epfl.ch/record/161515/files/04598375.pdf

To be continued…

http://www.tuks.nl/ Arend Lammertink

Bijzonder interessant. Het mechanisme waar het om lijkt te draaien heet Brillouin scattering:

http://en.wikipedia.org/wiki/Brillouin_scattering

-:- As described in classical physics, when the medium is compressed its index of refraction changes, and a fraction of the traveling light wave, interacting with the periodic refraction index variations, is deflected as in a three-dimensional diffraction grating. Since the sound wave, too, is travelling, light is also subjected to a Doppler shift, so its frequency changes. -:-

Merk op dat het hier gaat om een mechanische compressie van het medium, en voor zover me nu duidelijk is wordt dit gedaan met behulp van geluidsgolven.

Uit het artikel in mijn vorige post: -:- Among all parametric processes observed in silica, stimulated Brillouin scattering (SBS) turns out to be the most efficient. In its most simple configuration the coupling is realized between two optical waves propagating exclusively in opposite directions in a single mode fibre, through the stimulation by electrostriction of a longitudinal acoustic wave that plays the role of the idler wave in the interaction [4]. This stimulation is efficient only if the two optical waves show a frequency difference giving a beating interference resonant with an acoustic wave (that is actually never directly observed). This acoustic wave in turn induces a dynamic Bragg grating in the fibre core that diffracts the light from the higher frequency wave back into the wave showing the lower frequency. -:-

Interessant detail is dat het hier gaat om silica. Dit is natuurlijk gewoon glas, maar het is wel een silicium oxide en silicium is een halfgeleider. En wat hier gebruikt wordt is de kristallijne vorm:

http://nl.wikipedia.org/wiki/Siliciumdioxide

-:- Silicium(di)oxide of silica is het bekendste oxide van silicium.

In de natuur komt het in diverse vormen voor, zowel in kristallijne als niet-kristallijne (amorfe) vorm. Kwarts is een voorbeeld van kristallijn silica, andere voorbeelden zijn cristobaliet en tridymiet. Opaal is een voorbeeld van amorf silica net als door extreme hitte samengesmolten kwarts (kwartsglas). -:-

Het artikel van Stenner “The speed of information in a ‘fast-light’ optical medium” over group velocity, etc. kan hier gevonden worden:

http://www.phy.duke.edu/research/photon/qelectron/pubs/StennerNatureFastLight.pdf

“One consequence of the special theory of relativity is that no signal can cause an effect outside the source light cone, the space-time surface on which light rays emanate from the source1. Violation of this principle of relativistic causality leads to paradoxes, such as that of an effect preceding its cause2. Recent experiments on optical pulse propagation in so-called ‘fast-light’ media—which are characterized by a wave group velocity u g exceeding the vacuum speed of light c or taking on negative values3—have led to renewed debate about the definition of the information velocity u i. One view is that u i 5 u g (ref. 4), which would violate causality, while another is that u i 5 c in all situations5, which would preserve causality. Here we find that the time to detect information propagating through a fast-light medium is slightly longer than the time required to detect the same information travelling through a vacuum, even though u g in the medium vastly exceeds c. Our observations are therefore consistent with relativistic causality and help to resolve the controversies surrounding superluminal pulse propagation.”

Een heel klein voorbeeld van hoe het er nu echt bij staat bij de gevestigde tijdschriften is dit stukje uit het abstract van het artikel van Stenner, nota bene in Nature:

"Recent experiments on optical pulse propagation in so-called ‘fastlight’ media—which are characterized by a wave group velocity v_g exceeding the vacuum speed of light c or taking on negative values—have led to renewed debate about the definition of the information velocity v_i. One view is that v_i = v_g (ref. 4), which would violate causality, while another is that v_i = c in all situations, which would preserve causality."

Nu is de group velocity v_g dus de snelheid van de omhullende van een zich voortplantend signaal, waar normaal gesproken de informatie in zit. Wikipedia heeft een leuk plaatje met een animatie waarbij de groep snelheid negatief is ten opzichte van de fase snelheid, de draaggolf:

http://en.wikipedia.org/wiki/Group_velocity

De draaggolf (fase snelheid) beweegt naar links, de omhullende (groep snelheid) beweegt naar rechts.

En nu krijgt Nature het dus voor elkaar een artikel te publiceren waarin beweerd wordt dat een negatieve groepssnelheid een schending van causaliteit zou zijn. Want het signaal bevindt zich eerder op de “uitgang” dan op de “ingang”. Dit zijn toch gewoon denkfouten van Sesamstraat niveau?

Ik bedoel: als de omhullende de andere kant op beweegt dan de draaggolf, dan gaat die omhullende toch gewoon van de andere kant je glasvezel IN en komt er aldus enige tijd later weer UIT en wel aan de kant die je vanuit de draaggolf als INgang ziet. Maar het ding beweegt dus gewoon achteruit t.o.v. de voortbeweging van de draaggolf en dus bevindt hij zich eerst op het einde dat je vanuit de draaggolf gezien als uitgang bestempelt en pas later op het einde dat je vanuit de draaggolf bezien als ingang bestempelt…

Stenner et al

http://en.wikipedia.org/wiki/Dispersion_%28optics%29

''Another consequence of dispersion manifests itself as a temporal effect. The formula v = c / n calculates the phase velocity of a wave; this is the velocity at which the phase of any one frequency component of the wave will propagate. This is not the same as the group velocity of the wave, that is the rate at which changes in amplitude (known as the envelope of the wave) will propagate.

When we take a look at the WikiPedia page on group velocity, we find a picture which shows the group velocity as the velocity of the signal as in an AM modulated signal on a carrier wave:

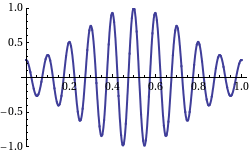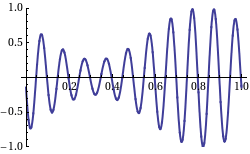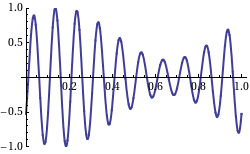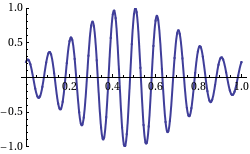
This shows a wave with the group velocity and phase velocity going in different directions[1] . The group velocity is positive (i.e., the envelope of the wave moves rightward), while the phase velocity is negative (i.e., the peaks and troughs move leftward).

Not that in this picture, the "carrier wave" moves from right to left, and the "AM" signal from left to right. So, this is what a negative group velocity would like of we were capable of creating such a signal with radio waves, which would require heterodyning of a number of (carrier) waves.

Now let's continue with the optical dispersion page:

For a homogeneous medium, the group velocity vg is related to the phase velocity by (here λ is the wavelength in vacuum, not in the medium):''
The group velocity vg is often thought of as the velocity at which energy or information is conveyed along the wave. In most cases this is true, and the group velocity can be thought of as the signal velocity of the waveform. In some unusual circumstances, called cases of anomalous dispersion, the rate of change of the index of refraction with respect to the wavelength changes sign, in which case it is possible for the group velocity to exceed the speed of light (vg > c). Anomalous dispersion occurs, for instance, where the wavelength of the light is close to an absorption resonance of the medium.

So, according to the main stream interpretation, under certain conditions having to do with "resonance" (and thus "heterodyning") an anomaly occurs, which is called "anomalous dispersion".

When the dispersion is anomalous, however, group velocity is no longer an indicator of signal velocity. Instead, a signal travels at the speed of the wavefront, which is c irrespective of the index of refraction. Recently, it has become possible to create gases in which the group velocity is not only larger than the speed of light, but even negative. In these cases, a pulse can appear to exit a medium before it enters. Even in these cases, however, a signal travels at, or less than, the speed of light, as demonstrated by Stenner, et al.

Now let's get this straight. The anomaly is that we get a negative group velocity, which supposedly is no longer an indicator of signal velocity, but it is an accepted fact that it is possible to create a situation whereby the group velocity exceeds c or becomes negative. Now when the group velocity becomes negative, we get something which is considered to be very strange: "a pulse can appear to exit a medium before it enters".

In other words: when we get a negative group velocity, which would normally considered to be the signal velocity, we get the situation that what normally would be considered "the signal" appears FIRST at "the exit" of the medium and some time later at the "entrance" of the medium, which is what you would "normally" expect IF you would consider the group velocity to be equal to the signal velocity. You see, IF the signal velocity equals the negative group velocity, well, then the signal would go the other way as your carrier wave and thus appears FIRST at the "exit" and LATER at the "entrance". Sesame Street level logic, I should think.

So, the anomaly is that signals, when considered along "normal" Sesame Street level logic, can be experimentally shown to propagate FASTER than the speed of light. And THAT is a problem, because according to Einstein's theory, that is impossible. So, what to do? Announce to the world that you have experimental proof that Einstein's theory is incorrect?

http://infoscience.epfl.ch/record/128303/files/ApplPhysLett_87_081113.pdf

http://www.tuks.nl/pdf/Reference_Material/Fast_Light/Gonzalez-Herraez%20et%20al%20-%20Optically%20controlled%20slow%20and%20fast%20light%20in%20optical%20fibers%20using%20stimulated%20Brillouin%20scattering%20-%202005.pdf

Abstract:

We demonstrate a method to achieve an extremely wide and flexible external control of the group velocity of signals as they propagate along an optical fiber. This control is achieved by means of the gain and loss mechanisms of stimulated Brillouin scattering in the fiber itself. Our experiments show that group velocities below 71 000 km/ s on one hand, well exceeding the speed of light in vacuum on the other hand and even negative group velocities can readily be obtained with a simple benchtop experimental setup. We believe that the fact that slow and fast light can be achieved in a standard single-mode fiber, in normal environmental conditions and using off-the-shelf instrumentation, is very promising for a future use in real applications.

Successful experiments to widely control the light group velocity have been widely reported these past few years, 1 showing the possibility to slow the speed of light up to nearly stopping it 2,3 or to achieve group velocity exceeding the vacuum light velocity c. 4,5 Strong negative group velocities have also been demonstrated. 6 But all these experiments use special media like cold atomic gases 4–6 or electronic transitions in crystal- line solids 7 working at well defined wavelengths.

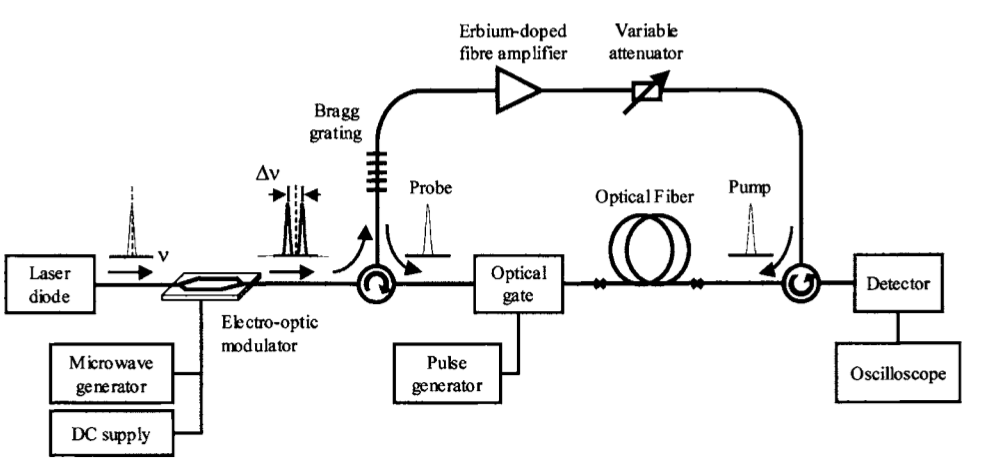
Stimulated Brillouin scattering (SBS) is usually described as the interaction of two counterpropagating waves, a strong pump wave, and a weak probe wave. If particular phase matching conditions are met (namely $ f_{Pump} = f_{probe} + \nu_B$, $\nu_B$ being the Brillouin shift), an acoustic wave is generated. This acoustic wave scatters photons from the pump to the probe wave, stimulating the process.

https://en.wikipedia.org/wiki/Brillouin_scattering

Brillouin scattering, named after Léon Brillouin, refers to the interaction of light and material waves within a medium. It is mediated by the refractive index dependence on the material properties of the medium; as described in optics, the index of refraction of a transparent material changes under deformation (compression-distension or shear-skewing).

The result of the interaction between the light-wave and the carrier-deformation wave is that a fraction of the transmitted light-wave changes its momentum (thus its frequency and energy) in preferential directions, as if by diffraction caused by an oscillating 3-dimensional diffraction grating.

If the medium is a solid crystal, a macromolecular chain condensate or a viscous liquid or gas, then the low frequency atomic-chain-deformation waves within the transmitting medium (not the transmitted electro-magnetic wave) in the carrier (represented as a quasiparticle) could be for example:

  • mass oscillation (acoustic) modes (called phonons);
  • charge displacement modes (in dielectrics, called polarons);
  • magnetic spin oscillation modes (in magnetic materials, called magnons).

acoustic mass oscillation == longitudinal dielectric wave :)

[...]

From the perspective of solid state physics, Brillouin scattering is an interaction between an electromagnetic wave and one of the three above-mentioned crystalline lattice waves. The scattering is inelastic i.e. the photon may lose energy (Stokes process) and in the process create one of the three quasiparticle types (phonon, polaron, magnon) or it may gain energy (anti-Stokes process) by absorbing one of those quasiparticle types. Such a shift in photon energy, corresponding to a Brillouin shift in frequency, is equal to the energy of the released or absorbed quasiparticle. Thus, Brillouin scattering can be used to measure the energies, wavelengths and frequencies of various atomic chain oscillation types ('quasiparticles'). To measure a Brillouin shift a commonly employed device called the Brillouin spectrometer is used, the design of which is derived from a Fabry–Pérot interferometer.

[...]

Contrast with Rayleigh scattering

Rayleigh scattering, too, can be considered to be due to fluctuations in the density, composition and orientation of molecules within the transmitting medium, and hence of its refraction index, in small volumes of matter (particularly in gases or liquids). The difference is that Rayleigh scattering involves only the random and incoherent thermal fluctuations, in contrast with the correlated, periodic fluctuations (phonons) that cause Brillouin scattering. Contrast with Raman scattering

Raman scattering is another phenomenon that involves inelastic scattering of light caused by the vibrational properties of matter. The detected range of frequency shifts and other effects are very different compared to Brillouin scattering. In Raman scattering, photons are scattered by the effect of vibrational and rotational transitions in the bonds between first-order neighboring atoms, while Brillouin scattering results from the scattering of photons caused by large scale, low-frequency phonons. The effects of the two phenomena provide very different information about the sample: Raman spectroscopy can be used to determine the transmitting medium's chemical composition and molecular structure, while Brillouin scattering can be used to measure the material's properties on a larger scale – such as its elastic behaviour. The frequency shifts from Brillouin scattering, a technique known as Brillouin Spectroscopy, are detected with an interferometer while Raman scattering uses either an interferometer or a dispersive (grating) spectrometer.

Stimulated Brillouin scattering

For intense beams of light (e.g. laser) travelling in a medium, such as an optical fiber, the variations in the electric field of the beam itself may induce acoustic vibrations in the medium via electrostriction or radiation pressure. The beam may display Brillouin scattering as a result of those vibrations, usually in the direction opposite the incoming beam, a phenomenon known as stimulated Brillouin scattering (SBS). For liquids and gases, the frequency shifts typically created are of the order of 1–10 GHz resulting in wavelength shifts of ~1–10 pm in the visible light. Stimulated Brillouin scattering is one effect by which optical phase conjugation can take place.

https://en.wikipedia.org/wiki/Phonon

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids. Often designated a quasiparticle,[1] it represents an excited state in the quantum mechanical quantization of the modes of vibrations of elastic structures of interacting particles.

Phonons play a major role in many of the physical properties of condensed matter, like thermal conductivity and electrical conductivity. The study of phonons is an important part of condensed matter physics.

The concept of phonons was introduced in 1932 by Soviet physicist Igor Tamm. The name phonon comes from the Greek word φωνή (phonē), which translates to sound or voice because long-wavelength phonons give rise to sound. Shorter-wavelength higher-frequency phonons are responsible for majority of the thermal capacity of solids.

[...]

Definition

A phonon is a quantum mechanical description of an elementary vibrational motion in which a lattice of atoms or molecules uniformly oscillates at a single frequency.[2] In classical mechanics this designates a normal mode of vibration. Normal modes are important because any arbitrary lattice vibration can be considered to be a superposition of these elementary vibration modes (cf. Fourier analysis). While normal modes are wave-like phenomena in classical mechanics, phonons have particle-like properties too, in a way related to the wave–particle duality of quantum mechanics.

[...]

Acoustic phonons are coherent movements of atoms of the lattice out of their equilibrium positions. If the displacement is in the direction of propagation, then in some areas the atoms will be closer, in others farther apart, as in a sound wave in air (hence the name acoustic). Displacement perpendicular to the propagation direction is comparable to waves in water. If the wavelength of acoustic phonons goes to infinity, this corresponds to a simple displacement of the whole crystal, and this costs zero energy. Acoustic phonons exhibit a linear relationship between frequency and phonon wavevector for long wavelengths. The frequencies of acoustic phonons tend to zero with longer wavelength. Longitudinal and transverse acoustic phonons are often abbreviated as LA and TA phonons, respectively.

Optical phonons are out-of-phase movements of the atoms in the lattice, one atom moving to the left, and its neighbour to the right. This occurs if the lattice basis consists of two or more atoms. They are called optical because in ionic crystals, like sodium chloride, they are excited by infrared radiation. The electric field of the light will move every positive sodium ion in the direction of the field, and every negative chloride ion in the other direction, sending the crystal vibrating. Optical phonons have a non-zero frequency at the Brillouin zone center and show no dispersion near that long wavelength limit. This is because they correspond to a mode of vibration where positive and negative ions at adjacent lattice sites swing against each other, creating a time-varying electrical dipole moment.

https://nl.wikipedia.org/wiki/Fonon

Een fonon is een gekwantiseerde collectieve trillingswijze van een kristal.

In een kristallijn materiaal zijn de atomen en/of moleculen via wisselwerkingen van wisselende sterkte aan elkaar gekoppeld. In sommige structuren, zoals in diamant, zijn dit sterke covalente bindingen, in andere zoals vast argon (bij lage temperatuur) zijn het slechts zwakke vanderwaalswisselwerkingen. De meeste materialen nemen een tussenpositie in.

In een los molecuul kan men vaak de trillingswijzen van de afzonderlijke bindingen in eerste instantie als een harmonische oscillator beschrijven. Bij grotere moleculen ontstaan er echter trillingswijzen die meerdere atomen en hun bindingen omvatten. Bij een vaste stof moet men in de regel alle atomen van het gehele kristal in hun geheel beschouwen. De natuurlijke trillingswijzen van zo'n systeem kunnen dan het beste in termen van Bloch-functies (sinusoïdale golven) beschreven worden. De golven worden gekenmerkt door een golfvector k in een beschrijving die analoog is aan die van de elektronenbanden van het kristal.

De energie van de trilling E(k) is een functie van de waarde van k en men kan deze functie als een band van trillingswijzen beschouwen. Omdat er meestal meer dan één atoom in een eenheidscel van de structuur zit, zijn er in het algemeen voor iedere waarde van de golfvector een aantal verschillende trillingswijzen met verschillende symmetrie.

Iedere trillingswijze kan afzonderlijk als een gekwantiseerd systeem beschouwd worden. Zo'n kwantum wordt fonon genoemd. Omdat fononen bosonen zijn kan een bepaalde trillingswijze meer dan een keer tegelijk aangeslagen worden.

"omdat fononen bosonen zijn..."

https://nl.wikipedia.org/wiki/Boson_%28deeltje%29

Een boson (genoemd naar Satyendra Nath Bose) is een deeltje dat een heeltallige spin bezit (0, 1, 2, ...). Dit in tegenstelling tot een fermion, dat een halftallige spin heeft (1/2, 3/2, 5/2, ...).

De volgende deeltjes zijn bosonen: 

    de ijkbosonen die de vier fundamentele natuurkrachten dragen:
        Voor het elektromagnetisme het foton
        Voor de zwakke kernkracht het W-boson en het Z-boson
        Voor de sterke kernkracht het gluon
        Voor de zwaartekracht het (nog niet aangetoonde) graviton
    samengestelde deeltjes met een even aantal fermionen, bijvoorbeeld

mesonen.

Een bijzonder boson is het higgsboson, een boson dat onderdeel is van het standaardmodel van de deeltjesfysica en dat verantwoordelijk zou zijn voor de massa van elementaire deeltjes.

Bosonen kunnen zich, in tegenstelling tot fermionen, in dezelfde kwantumtoestand bevinden en blijken niet te voldoen aan het uitsluitingsprincipe van Pauli. Bosonen voldoen aan de Bose-Einsteinstatistiek en hebben daardoor bijzondere eigenschappen, zoals het kunnen vormen van een Bose-Einsteincondensaat.

Een voorbeeld hiervan is het 4heliumatoom. Dit is een boson, want het bestaat uit een even aantal fermionen. Bij zeer lage temperatuur wordt het helium supervloeibaar. In deze merkwaardige toestand heeft de vloeistof geen viscositeit en geen oppervlaktespanning. Een bekertje met supervloeibaar helium kan daardoor zonder ogenschijnlijke aanleiding leeglopen doordat het helium over de rand kruipt om de toestand met laagste energie op te zoeken.

Bosonen spelen ook een rol in supergeleiding, waar twee elektronen samen een boson vormen, een Cooperpaar.