This paper is only an overview and first step in a very large undertaking: overhauling QCD. I will not be able to list all the corrections here, of course. That would require a book. At this time, I only intend to critique QCD very broadly, and to very broadly show the method for fixing it.

My first task here—showing that QCD is a very bald heuristics—is not a difficult one. Anyone who looks at QCD for more than a few hours will discover that most of the words in QCD are mechanically unassigned. The founders of QCD embraced this fact from the beginning, making no effort to hide it. That is why they chose words that displayed this heuristic character very plainly, with whimsical characteristics that were flagrantly non-mechanical. And so we have quarks with color, strangeness, charm, flavor, and so on.* Now, 40 years later, we have much more data, but we have not seen a mechanical explanation of the numbers. We have not seen this explanation because no one demands it or desires it: all are satisfied with the math and the terms.

In order to obtain such relations that we conjecture to be true, we use the method of abstraction from a Lagrangian field-theory model. In other words, we construct a mathematical theory of the strongly interacting particles, which may or may not have anything to do with reality, find suitable algebraic relations that hold in the model, postulate their validity, and then throw away the model. We may compare this process to a method sometimes employed in French cuisine: a piece of pheasant meat is cooked between two slices of veal, which are then discarded.³

That's very clever, but I don't see any physics there. Ask yourself why contemporary physics is so keen to avoid "reality". No matter whose book you are reading, whether it is Gell-Mann's or Feynman's or Hawking's, you see this same sort of sentence. "We are not concerned with reality, because we don't claim to know anything about reality; we only want to match the math to the experiment." They not only state this very strange idea out loud, they parade it as a bold piece of theorizing. But ask yourself what, precisely, is bold about it. Is it really boldness, or is it cowardice? To me, physicists avoiding reality is not a sign of great boldness or invention. It is a ploy, a clever misdirection in order to avoid troublesome questions. The physicist is acting more like an attorney here than a scientist. A scientist would naturally be interested in reality, since that is what science is about. Only a sophist posing as a scientist would think of trying to convince you that reality is of no importance. Notice that Gell-Mann is not only fleeing reality, he is also fleeing the confines of his own math. He has created a mathematical model, in order to skirt any questions of reality, then he has thrown away the model, too. That is like explaining A with B, then throwing B away. What do you have at the end? You have neither A nor B. You have no tasty pheasant or fatty veal, you have a sandwich of air. That would seem to be non-productive and hunger-inducing, but it is just what the contemporary physicist wants. You see, a theory of air cannot be critiqued. Try critiquing a cloud: there is nothing to grab onto. Just as a good attorney is infinitely slippery, so is the contemporary physicist. He is not a pheasant or a baby cow, he is an eel. Gell-Mann has created a theory that looks like something, but that is really nothing.

Wikipedia brags that “there is a huge body of experimental evidence for QCD,”—and this brag is at the top of the page on QCD—but near the bottom of the page, we find the astonishing admission that quantitative tests of non-perturbative QCD are few in number. We even find an “unsolved problems” section, in which we find this bombshell:

The equations of QCD remain unsolved at energy scales relevant for describing atomic nuclei.

The writer pretends this is a problem of “confinement” [see below], but it is a much bigger problem than that. It would be analogous to admitting that Newton’s gravitational equation “remains unsolved at energy scales relevant for describing planetary orbits.”

So both the terms and the overall theory of QCD are non-mechanical. As another example, all physicists will admit that color is a “hidden” variable—that is, unassignable to any known or theorized physical or mechanical property of the quark. But most of the other words (quark quantum numbers or “flavors”) are equally unassignable. When a quantum physicist says that quark spin is assignable, for instance, he only means that we have built a table for it and added to the matrix. He does not mean that the quark is spinning in any known way, expressed by that number.

Quarks have a spin of 1/2. What does that mean, mechanically? Does it mean the quark is spinning half as fast as some other fundamental particle, or that it is spinning with a halved amplitude or frequency, or a halved angular momentum? No one knows. I don’t believe that anyone (but me) cares. [See my paper on Stern-Gerlach for a full analysis of this.] Spin, like the strangeness number (S) and the baryon number (B) and so on, is mechanically unassigned. Wikipedia puts it this way: “elementary particles are believed to be point-like and so they cannot rotate around themselves.” Most or all of these variables are hidden to very large degrees, in a mechanical sense, and the quark numbers are mainly tweeked with each new discovery, to keep the tables symmetrical and internally consistent, according to the manufactured rules of the theory.

The last quote above from Wiki brings up another problem. If quarks are point-like and cannot spin in a physical sense, what does chirality and symmetry apply to at this level? We have quarks that are right-handed and left-handed in various ways, we are told, and some interactions preserve symmetry and others don’t. But what is moving clockwise or counter-clockwise, expressing right or left “handedness” if not real spin? How can a point express chirality, and how can a point be either symmetrical or non-symmetrical? To speak of symmetry or non-symmetry logically requires heterogeneity. It is illogical to assign chirality or symmetry to a point.

I will remind you that quarks have never been seen in bubble chambers, ionization chambers, or any other experiments. Quarks, along with all their quantum numbers, are wholly theoretical. They go part of the way in explaining experiments; we have no better theory; so we continue to tweek what we have. It is said that all the various quarks have now been “discovered,” but this does not mean they have tracks in bubble chambers all to themselves. It means that mesons have been discovered that come close to energy predictions. For instance, the meson sometimes called the charmonium was the particle detected as “proof” of the charm quark. But the charm quark was never seen: only the proposed pair.

This is true of all quarks. No quark had been confirmed with a visible and singly assignable track. As with the bulk of string theory, the complete non-arrival of the fundamental objects has not deterred anyone. In fact, one might say that the invisibility of the guest of honor is a necessary feature of the party. We are told that quarks are unstable outside the nucleus, but this is just a bald assertion, with no theory to back it up. Notice that we are never told why the quark should be so unstable, or more unstable than the other very unstable exotics in the quantum zoo. For example, we have managed to produce proof of the W boson—at least enough proof to convince insiders—though the W boson only lives for 10^-27 seconds. Why should the quark be less stable than that? Both particles are normally buried in the nucleus, and the W is a mediating particle. It would seem it should be more fleeting than the quarks it mediates, not less.

Wikipedia addresses this question in passing (since the standard model itself only addresses it in passing). Wiki admits, “There is no analytic proof that QCD should be confining,” which means there is no reason that the quarks should be confined to the nucleus, even in high-energy collisions, but Wiki continues:

Intuitively, confinement is due to the force-carrying gluons having color charge. As any two electrically charged particles separate, the electric fields between them diminish quickly, allowing electrons to become unbound from nuclei. However, as two quarks separate, the gluon fields form narrow tubes (or strings) of color charge, which tend to bring the quarks together as though they were some kind of rubber band. . . . When two quarks become separated, as happens in particle accelerator collisions, at some point it is more energetically favorable for a new quark/anti-quark pair to spontaneously appear out of the vacuum, than to allow the quarks to separate further. As a result of this, when quarks are produced in particle accelerators, instead of seeing the individual quarks in detectors, scientists see "jets" of many color-neutral particles (mesons and baryons), clustered together. This process is called hadronization, fragmentation or string breaking, and is one of the least understood processes in particle physics.¹

“Gluons carrying tubes of color charge” as the mechanism of confinement is so outlandish it is difficult to believe it is paraded in the open as a scientific explanation. Physicists no longer know when to keep quiet. Are these tubes like the tubes of paint in a painter’s box: does the gluon also carry a palette and brushes and a little bottle of turpentine, for clean-up jobs? And as for the rest, how does anyone know it is more “energetically favorable” to create quark-anti-quark pairs than to allow quarks to separate further? That is not a scientific statement. If we don’t know the energy of each event, how can we know which is more energetically favorable? And we can’t know the energy of each event, since we are told one event—quark separation—is impossible. This physicist implies that it is feasible to measure the energy difference between an unknown event and an impossible event! By this logic, any seen event must be more “energetically favorable” than any unseen event, and we can propose that things happen as they do because the energy was favorable. Yes, the quarks just have the wrong ch’i.

The only fresh air here is the admission that hadronization is not well understood, although I don’t know why they aren’t able to make up something. The rest of the explanation is manufactured from nothing: why not manufacture a longwinded answer for hadronization, and pass it off as bedrock?

There is no analytical or theoretical reason that the quark should remain hidden. Conversely, there is every reason to think that the quark’s non-discovery should be a very big problem for the standard model. In any other field, and at any other time in history, a theory with such a giant, obvious hole in it would have major problems. A theory of cats without a cat would not be a strong theory. A theory of unicorns without a unicorn would not be a strong theory. But, for some reason, a theory of quarks with no quark is one of the most famous and feted theories of the 20^th century. I suggest to you that this is a measurement of the health of the field, and of the independence of those that inhabit it. How can it be that physicists are allowed to theorize with no least amount of criticism? On the contrary, the method now appears to be that a high-level person in some prestigious physics department comes up with a theory, and everyone immediately goes to work seeking confirmation of it. No one goes to work trying to show that it is a pathetic mess of illogic and question begging, although in most cases that is precisely what it is.

The decades of collision experiments in QCD have been very useful. I do not wish to imply that no good work has been done. Even the given theory of chromodynamics may be said to be a useful first step, in that it catalogues all the interactions and provides tentative variable assignments. But as a piece of mechanics or dynamics, it is threadbare.

One might say that chromodynamics, like electrodynamics, has mainly suffered from a lack of patience. Like QED, QCD has seen its data far outstrip its theory. QM and QED were built on the back of a woefully incomplete E/M theory, as I have shown. If we stick to the standard model, we still have no idea how to explain the E/M field mechanically, at a foundational level. The theory of positive and negative charges, mediated by virtual or messenger photons, is a mechanical disaster. Despite this, QM and QED found it necessary to explain more and more complex interactions, at smaller sizes. Quantum physicists did this by pasting together more and more math, and by ignoring mechanics more and more the farther along this path they went. Early on, the big names gave up on theory as mechanics, and said so out loud. Bohr and Heisenberg, in the infamous Copenhagen Interpretation, announced that mechanics, as a logical explanation, was categorically impossible. From that point, we could hope to have math, but we could not hope to have mechanics. We could not hope for a logical, physical explanation. This attitude has remained up to the present moment, transferred through Pauli and Dirac and then through Feynman and Gell-Mann, and now personified by most living physicists in most current physics departments.

From its inception, QCD followed this program precisely, continuing to ignore mechanics and dynamics and kinematics. It continued to use these old words, since they carried prestige and provided a feeling of solidity. But, by the old definitions, there is no mechanics in quantum mechanics, and no dynamics in quantum chromodynamics. There are only the math and vocabulary.

QCD had to be built on the back on QED, but the back of QED was broken to start with. QED’s back was broken because it inherited the fields of Faraday and Maxwell, and never clarified them. E/M has no foundation, which gives QED no foundation, which gives QCD no foundation. And we have now built our structure to such a height—we are so far above the ground—that we may be said to be floating upon thin air.

Ironically, QCD has suffered from two opposite syndromes. I have just shown how the data outstripped the theory: QCD had to be built on the back of very incomplete E/M, QM, and QED theories. But the theory also outstripped the data. It did this by once again rushing. QCD was not patient enough to fill in the gaps in QM and QED before it began theorizing in its own arena; and it was not patient enough to wait for data from accelerators before it began theorizing fundamental particles and interactions. Gell-Mann and Zweig first proposed quarks in 1964, four years before the first major experiment at SLAC showed fine structure to the proton. They had fairly solid reasons for proposing some sort of substructure to the proton, but no solid reasons for supposing this substructure must be made up of discrete particles. Interestingly, there was not then any competing theory, that I know of: a theory that would propose internal spins or motions instead of particles (as mine does). The understanding of the mechanics of spin has always been so partial that no one ever once suggested any serious counter-theory to quarks, and no one has to this day. The most serious alternative to quarks was Feynman’s theory of partons, but it did not differ greatly from the Gell-Mann/Zweig model, and so was soon absorbed by it. Earlier theoretical attempts, like those of Sakata, are also not of the wave variety, relying instead—like all later attempts—on a non-mechanical interpretation of the data.

Because the theory of QCD predated the data, the data was read to fit the theory. This is the way of modern physics, and I have already shown how it has effected the theory of black holes, among other things. But this method must be topsy-turvy. When you have a hammer in hand, everything starts to look like a nail. When you have a new theory—built from near-zero data—everything begins to look like confirmation of it. From the beginning, QCD got very little critique and very much effort at proof. As soon as the major accelerators went online with their new energies, they were put to use seeking confirmation of QCD. If a new particle was theorized, it was immediately sought. If a new particle was discovered, the theory was immediately tweeked to include it. No one wanted to disprove the theory and everyone wanted to prove it. Is it any wonder that it has stood so well? Forty years later, no one is seriously bothered by the non-appearance of the quark (or of the Higgs boson, etc.). Most have accepted that the quark is infinitely unstable, and they will not be bothered if we never find it. And one assumes they will find some way to feel good about the non-appearance of the Higgs boson, even after we exhaust 200 or 300GeV limits. QCD will then borrow the apologetics of string theory, claiming that a particle with the mass of a grain of sand is too unstable to be found. Of course this will not stop them from using tax dollars to build even larger colliders, to seek other hypothetical particles.

One begins to think that, given the lack of critical thinking among physicists and science readers, it is no longer necessary to hide gaping theoretical holes. No one has any desire to see problems, and so they are guaranteed not to. They embrace the non-mechanical whimsies of QCD and dance about, fully prepared to waltz with any pretty paradox. Hence the open-armed welcome of string theory.

QCD is like string theory in another way: string theory has conveniently pushed all possible proof to the 10¹⁹ GeV energy range, and QCD has followed suit by continuing to push its experimental proofs to higher and higher energies. This trick forces the math to carry all the weight, and that is just how new physics wants it. These energies are permanantly out-of-reach, and this is no accident. It gives physicists the excuse to build an infinite line of bigger machines, based only on promises, and prevents any final tally of the theory. No one ever asks, "Look, what actual problems have you solved, even theoretical problems? Let us go back to 1900, look at all the theory since then, and see if it has solved more problems or created more problems. Has it even solved any of the problems it has created?" With these high energies, physicists keep everyone's eyes on the future. They keep them from making present demands on the theory: that it solve problems we have now.

Yes, modern physics depends on its math and its machines. Both deflect current criticism. Regarding the math, QCD, like other modern theories, has doubled and tripled its protection. It has warned physicists away from closely analyzing anything, taught them to do physics without serious logical analysis, and then built a Byzantine series of walls to prevent break-outs. QCD comes complete with its own very high walls. These walls provide insurance in those rare instances that anyone sobers up, pokes his head above ground and opens his eyes. These walls are mathematical walls, of course. As with Relativity and QED, all the heuristics of QCD are couched in a very difficult engineer’s math. The math is fairly glamorous in itself, and this deflects much of the potential disappointment or self-criticism from “physicists”, who like to be seen doing important things. Since theorists are not really doing theory anymore, and physicists are not really doing physics, by the old definitions, it is good that they can substitute pretty math for pretty theory, achieving equal or greater levels of prestige and causing equal or greater levels of awe among the laity.

As the perfect example of this, see Edward Witten, the top dog now in string theory. Witten's most impressive skill is as a mathematician, and he is the first physicist to win major mathematical medals. This is no accident. The mathematics departments love Witten, since he has continued to buy and import all their newest toys. Physics is not physics anymore, it is math. Like math, it is no longer proved by experiment or simple physical interaction, it is proved by the perceived "beauty of the edifice." Since mathematicians like bigger edifices, for their own sake, that is what we now get in physics. With QCD and string theory, physics is becoming "pure." It has long since lost its physical foundation (it lost that with the Copenhagen interpretation) and now it is little more than a flight of fancy, with (at times) a few rules of internal consistency.

I say engineer’s math because the math of QED and QCD is full of short cuts. Short cuts in math are good for efficiency, but are terrible for theory. Therefore, highly compressed math is great for engineers, but terrible for physicists. If you are doing mechanics (dynamics or kinematics), you want a very simple transparent math, with variables clearly assigned, no groupings of variables to confuse things, and all postulates right out in the open. But this is not what we see with quantum physics. QED and QCD are both buried under the Hamiltonian, to start with, and we must assume this is no accident. At its simplest, the Hamiltonian (H = Σpq - L) is a compression of the Lagrangian with a summation of the generalized momenta and position coordinates. The Lagrangian [L = Σ (T - V)] is a compression of the kinetic and potential energies. [See my more recent paper on the Lagrangian, where I show how it is fundamentally compromised.] So all individual mechanical variables—time, length, etc.—are buried very deep. In my overhaul, I will not only be throwing out all unnecessary particles and variables, I will be throwing out all unnecessary operators and algebras. The engineers can reintroduce the Hamiltonian and so on after we finish doing theory, to simplify their calculations. But for now, the math of QCD must be seen as one more wall to tear down.

This also applies to SU(3), which stands for special unitary group, a form of matrix math using Lie algebra. Just as it was never shown why the tensor calculus was necessary to Relativity, and it was never shown why complex numbers were necessary to E/M, and it was never shown why non-Euclidean math was necessary to gravity, it has never been shown why Lie albegra and matrix math is necessary to nuclear theory. In fact, SU(3) is not only unnecessary, it has proved impossible to apply. For example, one of these mathematical holes within the greater hole is called the Faddeev-Popov ghost. This ghost is a type of renormalization, and it requires adding ghosts fields to already calculated gauge fields, in order to make them consistent field theories. What this means is that the fancy math is known not to work. Just as in QED, the equations have to be pushed after the fact in various ways. Consistency is achieved only by fudging, since the data refuses to match postulates in a normal way. But rather than jettison these maths and start over, modern physicists prefer to keep them and plaster them up with chalk and band-aids. After all, it is the math that is the main draw, and if they ditched the pretty math and big book of terminology, 9/10’s of the sex-appeal of the field would evaporate. Physicists and science readers aren’t disturbed by things like Faddeev-Popov ghosts: they are thrilled by them. A house full of ghosts is so much more exciting than a house full of logic and reason.

But it remains a perhaps boring truth that these fancy maths are not necessary at all. These maths were invented in moments of ennui, by mathematicians who needed something to do, in order to advance their careers and to solve problems in more complex ways. The maths were brought into physics for the same reason. They act as novelty, misdirection, and brainwashing, all at the same time. If your eyes are on the math, your eyes are off the theory. If you are thrilling at ghosts, you are not analyzing the baseboards and the flooring. In graduate programs, they can’t answer your fundamental questions, and they have almost no real theory to teach you, so they must fill their days and your days somehow. They do this by teaching you these wordy and intricate maths. As Feynman bragged, it takes years to learn all the math. Yes, and during those years, you will have become a computing machine, incapable of independent thought or simple critique. With your formidable list of words and manipulations, you will feel secure, so secure that you will never notice that six foot hole next to your bed.

The truth is, like all the other physical problems of history, the problems of QCD can be solved with logical postulates and fairly simple math. Difficult math is not useful at the theoretical level. No, it is a menace, nothing less. I have proved this in my other papers, where I have solved difficult and embedded problems without any modern math, and done it in a fraction of the time. I will do the same here. I will not have time to pull apart the given math here (I may get to it later⁵), to show exactly what it is hiding and why, but if you want proof that I can do it, I send you to my explosion of complex numbers, where I show you precisely how they hide the holes in the E/M field.

I have already shown in another paper that the strong force is unnecessary. This proves how weak the entire structure of QCD must be. In this paper I will go beyond this, to show that we can also jettison the gluon, the boson, the weak force, and, yes, the quark itself. In this way, it may be that almost nothing of current theory will remain after our housecleaning but a few bricks clinging together in piles of rubble.

What allows for this overhaul are two fundamental and far-reaching discoveries. These discoveries are revolutionary, but shockingly simple. The first is that the E/M field is always repulsive at the foundational level. I have jettisoned attraction from all physics, and required all theory to be built on physical postulates. That is to say, I have resuscitated the original definitions of dynamics and kinematics. Interactions must be based on motions and forces by contact. It was thought that this could no longer be done, but I have shown that it can be done. I have shown that the motions of electrons relative to protons and fields can be explained without attractions, and I will show the same with particles within nuclei.

The second discovery arose from my study of superposition. In my paper on that subject, I showed that all the paradoxes of superposition could be explained simply by stacked spins, with each outer spin beyond the gyroscopic influence of inner spins. These stacked spins explained both the wave nature of all spinning particles as well as the famous anomalies of detectors. What I soon realized is that these stacked spins could be applied not only to electron or photons, but also to protons and neutrons. Once we apply these stacked spins to hadrons (baryons and mesons), we are able to explain particle breakups and particle compositions without quarks.

I will quickly gloss the findings of these earlier papers. Until now, spin (or angular momentum) has been treated as a generalizable parameter, theoretically equivalent to momentum or velocity or position. It turns out this mistake is based on the usually unstated assumptions of the new math (like the Lagrangian or Hamiltonian), where variables can be juggled willy-nilly, without any consideration of what is going on beneath the variables [see Gell-Mann quote above, where he calls the Lagrangian the "method of abstraction"]. I have also criticized this false attitude at length in various papers, but my criticism is proved in the problem of superposition, since spin cannot and must not be glossed over as just one more variable. It must be studied in depth, as mechanics. I have shown that a single spherical particle can have as many as four independent spins: 1) it can spin on its axis, 2) it can spin in the x-plane, as long as this second spin is outside the gyroscopic influence of the axial spin. That is, if the spinning sphere has a radius of 1, the x-spin must be end over end, with a length of 2. 3) It can spin in the y-plane, with a amplitude of 4, 4) it can spin in the z-plane, with an amplitude of 8. All these spins are strictly mechanical: that is, they could be built with real macro-particles as well as with quantum particles; and there is nothing esoteric or non-physical about them. And we can apply them to even the smallest quanta, since no particle is a point or point-like.

This analysis immediately explains Planck’s constant, for a start. Despite all the new math and theories, quantum physicists still do not understand the mechanical cause of quantization. This is it. Look at the equation E = hν. We see that energy is quantized because the frequency is quantized, and the frequency is quantized because the wavelength is quantized (frequency and wavelength are simple functions of one another). Well, these stacked spins are wavelengths. The x-spin is end-over-end, of magnitude 2 (if the radius is 1). Give the particle linear motion and this end-over-end spin creates the wavelength directly. That is, the wavelength is 2. All we have to notice beyond this is that we normally will be measuring only the outermost spin, the z-spin, so this will be the visible or electrical wavelength. If the radius is 1, then the z-spin will be 8. This gives us an easy way to calculate the size of the particle proper, given the measured electrical wavelength: just divide by 8.

To be clear, this explains quantization because all the wavelengths (x, y, and z) must be multiples of the axial spin or radius. Once again, this is simply to avoid gyroscopic interference of spins. We cannot have any fractions, much less a continuous increase, since only a doubling each time will take the spin beyond the influence of inner spins.

If we apply the spins to photons or electrons, we can explain the mysteries of quantization and superposition very easily and quickly and transparently. But if we apply them to hadrons, we can begin to explain the composition of nuclei, without any need of quarks. This is because the number of the degrees of freedom we achieve with such an analysis matches the degrees we achieve with quark theory [see just below], and the symmetry also matches current quark theory. Stacked spins replace the current quark quantum numbers, as well as explaining mechanically many things that have so far gone unexplained. Chirality and symmetry are given a physical basis, among many other things.

So these are the fundamental changes we have so far:

1) The mediating photons of charge are not virtual or “messenger.” There is no attraction. All charge is repulsive. Charge is mediated by B-photons, by straight bombardment. Not all particles must have charge, since not all particles must emit B-photons. Among particles with charge, this charge is a function of surface area. Therefore if we give the proton a charge of 1, the electron no longer has a charge of -1. It has a charge of about 1/1836 or .000545. The B-photon is also not mass-less and is not point-like. It has a calculable mass and radius, both of which are about G (6.67 x 10^-11) times the mass and radius of the proton. That is, the B-photon is eight million times smaller than the electron.

2) Gravity is a measurable force at the quantum level. It has been hidden in the mis-defined and mis-applied charge field. The total E/M or charge field we now measure at the quantum level is not a single field, but a unified field. Once we un-unify it, or separate it, we find the gravitational field as a major player once more. As at the macro-level, we find that gravity is strictly a function of radius. Mathematically, it may be treated as a straight expansion of the sphere of any given particle. Along with the new positive charge field, this explains relative attractions, orbital distances, and unification.

3) We have four possible spins on every quantum. A quantum may have all these spins, or only some of them. A quantum that loses an outer spin will seem to change from one quantum to another.

4) No strong force. No weak force. No gluons. No bosons.

Here is a list of possible spin states of a baryon.

+a+x+y+z

-a+x+y+z

+a-x+y+z

-a-x+y+z

+a+x-y+z

+a-x-y+z

-a+x-y+z

-a-x-y+z

+a+x+y-z

-a+x+y-z

+a-x+y-z

-a-x+y-z

+a+x-y-z

+a-x-y-z

-a+x-y-z

-a-x-y-z

Notice that we have 16 independent states. That this doubles the so-called “eightfold way”** of chromodynamics is no accident. In the matrix equations of Gell-Mann, also known as SU(3), we have 17 non-zero entries in the matrices (the last matrix had three entries). This is also not a coincidence.

As a start, you may think of the three x,y,z levels as replacing the up, down and strange quarks. The a-level then becomes the color variable. Because x, y, and z must have different energies, quarks appear to have different masses. But quark mass is a mirage. There are no quarks, and the mass differences are energy differences only.

According to this list, mesons are baryons stripped (during collision) of the outer spin. Mesons over the baryon mass are particles that have unstable spins on top of the stable z-spin.

The SLAC experiments in 1968 that showed substructure to the proton were showing not quarks, but spins. As we know, every particle is a wave, and we can now see that it is a wave with four possible inner structures. In a field or during inelastic scattering, inner spins will act like constituent particles, since they will have not only their own directional forces, they will have their own diameters which are less than the particle’s apparent diameter.

QCD has translated the three outer spins as three quarks. The axial spin is buried deep beneath the other three spins, and its radius is the actual radius of the particle, so it is “hidden.” It is this axial spin that has become “color” in QCD.

The proton and electron create the electrical field, via the linear energy of emission. The z-spin of the emission creates the magnetic field. The y and x-spins of all quanta are relatively buried, and are noticeable only in nuclear interactions. No known macro-forces are caused by them.

At very high energies, you can force other spins on top of the stable z-spin. These spins are highly unstable: the natural mass and radius of the particle cannot support it, and outer spins interfere with inner spins. These outer spins explain the appearance of quanta above the baryon energy. Since each spin doubles the apparent size of the particle (with a sphere radius of 1, a second x-spin creates a final wave amplitude of 16) and adds energy to it—and thereby mass—an exotic particle of this nature would appear large and massive. This explains W and Z particles. They are not bosons and are not responsible for any weak force: they are simply baryons with superadded spins. All of the energy for this new spin comes from the field, and in this sense the new particle is a temporary freak, not a mediating field particle.

To show this, let us take a fresh look at beta decay. According to the standard model, a neutron decays into a proton, an electron, and an electron antineutrino. It does this by first emitting a W boson. In accelerators, we “see” the first four particles in this decay, but we do not see the W boson. The W boson only lives for about 10^-27 seconds, we are told, so its track is too short to see, even did it exist (which is convenient, I would say). We believe in the W boson for theoretical reasons, and because the Feynman diagram tells us that it is the W boson that then decays into the electron and electron antineutrino. The theoretical reason we believe in it that we want very much to prove the existence of Higgs mechanisms and spontaneously broken symmetries, and we have been pursuing that for forty years (the new hadron collider is more money and time thrown in this direction). The reason we want to prove the Higgs mechanism and spontaneously broken symmetries goes far back into the history of QED, and is basically the attempt the cover our tracks for the past 80 years. In short, since the Copenhagen Interpretation forbade any mechanical talk about quantum particles, we could not provide for the mass of these particles in any classical way. This set up a chain of mistakes and mis-definitions and mis-assignments, which ultimately led to the illogical Higgs field. The Higgs field is basically a theoretical reductio, but no one wants to admit that, so we keep on funding supercolliders to prove the unprovable. The Higgs field is a field of virtual particles that underlie or make up the vacuum. For the vacuum to act like the vacuum, these virtual particles must obey symmetry: they can have charge over a very small interval, but the total charge must sum to zero. In the presence of matter, however, the vacuum breaks this symmetry, creating charge that does not sum to zero. This charge creates a force, which creates mass in the matter.

Now, any honest person could see that the Higgs field is non-mechanical and non-physical. It is something from nothing. Besides, it is a clear reductio. If you are going to assert that mass comes from nothing, in a bogus, non-mechanical fudge, why not just do it within matter? Why take the extra step and perform your magic trick on the vacuum? Why not perform it directly on matter? Why wave your magic wand over the vacuum, to create a force? Why not wave your magic wand over mass to give it mass, as Newton did? Higgs thought he was doing something clever by backing up a step, but I don’t see what he achieved. Honestly, all he achieved was another half-century of busy-work.

But mainstream physicists have been impressed with the Higgs field and gauge theory from the beginning. One must assume this is because it allowed them to create a new fudge of their own. This spontaneously broken symmetry was very suggestive to them, since they had a symmetry they needed broken as well, and they couldn’t see how to break it. As I have shown elsewhere, this “symmetry breaking” is really just fancy words for “fudging an answer.” These physicists had created a rule, convinced everyone of that rule, browbeaten thousands of graduate students into accepting that rule, and now they wanted to break it. In short, they needed to break the flavor symmetry, but chromodynamics didn’t allow it. Chromodynamics was symmetrical. To break this symmetry required they create a whole new force (the weak force) and two or three new particles. Once tied to the sexy Higgs field and gauge theory, this fourth fundamental force would be radical enough to go over the head of the old school, and to break the symmetry in an imposing and impressive way.

It looked like working at first, since it won the physicists Nobel Prizes, gave them book contracts, and made at least one of them, Weinberg, a household name. Unfortunately, the weak force and the W and Z particles depended on the Higgs boson, and the Higgs boson still has not been found, 40 years later. With each passing decade, this gets (or should get) more and more embarrassing, which is why we heard so much about the Superconducting Supercollider in the 80’s, and why we have to hear so much about the Hadron Collider now. The Higgs boson has now become “the god particle,” since according to the standard model, it creates everything—which will be all the more ironic when it turns out to be a ghost. We will need another Nietzsche to tell us that our god is dead. I volunteer, and begin now.

We don’t really have to study the electroweak theory or gauge theory or the Higgs field to see how tenuous and illogical this all was from the beginning. We only have to look at the Feynman diagram I described above. We are supposed to believe that the W boson decays into the electron and electron antineutrino. And we are supposed to believe that the W boson was emitted by the neutron. The problem is that the W boson has a mass of about 80 GeV/c², which is more massive than an iron atom. How is energy conserved in this emission and decay? Where does all that extra mass come from, and where does it go when we get down to the electron and electron antineutrino? 80GeV decays down to .5MeV? That is like saying that a marble emitted the Moon (while remaining a marble), and then the Moon decayed into a grain of sand and a whisper. Feynman’s diagram is incomplete, to say the least.

Is there a simpler way of explaining beta decay? Of course there is. We just have to return to my list of stacked spins and decide which one is the proton and which one is the neutron, and then go from there. We begin by taking the two most important facts known to us about neutrons. One, they have no charge; two, outside the nucleus they decay in about 15 minutes. Concerning the proton, we know that it has a charge and that it is stable. I have shown that charge is emission of B-photons, so the proton is emitting and the neutron is not. Why is the neutron not emitting? That is our first problem to solve mechanically. We will begin by assuming that all baryons emit equally (from the surface of the particle itself): this will save us from having to make up new rules for no reason. But we see that this emission must travel out from the surface of the particle through four stacked spins. It is clear that some combinations of spins allow the emission through and some don’t. Some combinations must block charge emission, and therefore charge. But how could they do this, in simple mechanical terms?

To see this, we simply follow the maze. To simplify the analysis, let us look at only one plane in the problem. We let the particle spin on its axis, and we define the x-dimension as the plane created by extending the equator. In this plane the particle is emitting photons like a pinwheel or spinning water sprinkler. To simplify even further, let us follow only one dt of emission. This emission will be a circle, obviously, one that is increasing in radius and decreasing in density. Now we add two motions: linear motion of the entire particle and end-over-end spin. To complete our analysis, we only have to add one more thing: the spin of the emitted photon. B-photons have wavelength and therefore spin just like any other particle. In this simplified analysis, we will look only at its outermost or z-spin, which we will define as clockwise.

Can we imagine any blocking at this point? No. In order to block anything with end-over-end spin, the particle would have to outrun its own emission. Since we assume the emission speed is c, this is an impossibility. Can we imagine any difference in +x or -x, that is, in clockwise end-over-end versus counter-clockwise end-over-end? No. There is no way that chirality could cause a mechanical difference at this point. Now we continue to the next level of spin. We encounter a larger end-over-end spin, of magnitude 4, in the y-plane. Can we imagine any blocking here? Again, no. So let us continue. We proceed to the next spin level, of magnitude 8, orthogonal to the others and outside their gyroscopic influence. Can we imagine any blocking here? Yes!

To show this in a simple illustration, let us transpose the fields into one plane, so that it can be drawn in photoshop. Let us try to draw the very first of the 16 possible combinations, that is +a+x+y+z. The initial emission from the surface of the particle will be straight out from the particle, in a line. Then, when we meet the next spin level, we must turn right or left. Let us assign right to “+”. In this combination, we have three right turns, which must bring us back to where we were, as you can see clearly.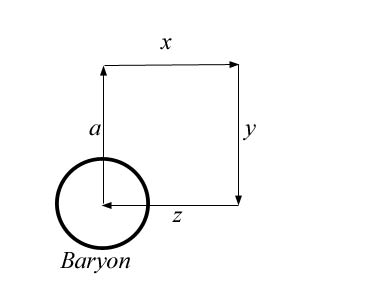

The emission is trapped by the stacked spins. It cannot escape the particle, and so the particle must be neutral. In this one-plane analysis, -a+x+y+z is also a neutron, since the last three turns are again right turns. Three left turns must also forbid emission in the same way, so +a-x-y-z and -a-x-y-z would also be neutrons.

Now, this analysis is a slight oversimplification, since we are only analyzing in one plane; but it shows you the method. If we do the full analysis, we find instead that these states are neutrons:²

-a-x-y+z -

+a+x+y-z -

-a+x+y-z -

+a-x-y+z -

They are neutrons for two reasons: 1) the emission cannot escape, and 2) the emission returns with the B-photons upside-down. That is what the last minus sign means here. Upside-down photons have a reversed spin, therefore they return opposite in every way to the way they were emitted from the surface of the particle: the energy is canceled completely.

These next states are anti-neutrons, since the returning spin of the radiation is not reversed. That is, the B-photons return upside-up:

+a-x+y+z +

+a+x-y-z +

-a-x+y+z +

-a+x-y-z +

Protons are:

+a+x+y+z

-a-x-y-z

-a+x+y+z

+a-x-y-z

Anti-protons are:

+a-x+y-z

-a+x-y+z

+a+x-y+z

-a-x+y-z

With the protons, the emission escapes from the stacked spins in the same state it was emitted from the surface of the particle. It has the same direction and chirality. With the anti-protons, the emission escapes in the same direction as it was emitted, keeping its full energy; but the emission is upside-down.

This means that the difference between particles and anti-particles is not a difference in the particles themselves, or in the size of the emission. The difference is in the combination of stacked spins. Certain combinations give us an emission field of B-photons that are spinning clockwise. Other combinations give us B-photons that are spinning counter-clockwise. When these two fields meet, they must cancel each other’s spins, and therefore each other’s repulsive energies. The particles emitting will therefore be unprotected: their fields are gone. They are prone to collision.

The neutron should also be prone to collision, since its B-photon field cannot get beyond its z-spin. But it is not as vulnerable to collision as some particles, since it retains its spins regardless. These spins are some protection, since they must be destroyed before the particle is “naked”. The z-spin has a lot of energy, whether B-photons are passing through it or not. This is the mechanical reason it survives for a short time outside the nucleus.

This is also the reason the neutron has more mass: it doesn’t lose the energy of emission. Since energy is mass, we may deduce that the mass equivalence of the emission of a baryon is 2.3 x 10^-30 kg. The neutron traps this emission; the proton emits it.

Finally, this also explains the slight mass difference between the neutron and anti-neutron, in a direct mechanical way. The emission is trapped by both particles, making them neutral; but in the anti-neutron, the trapped emission does not cancel its own energy precisely. A clockwise spin will cancel a counter-clockwise spin, when two particles of equal mass meet head-on. But if two particles of equal mass meet head-on, and each has a clockwise spin, the spin is not canceled. No, it is doubled. Which means that B-photons trapped in anti-neutrons cannot cancel out completely. Only their kinetic energy, or energy from forward motion, cancels. But the spin energy of the emission remains. Depending on which of the four anti-neutrons we are talking about, this spin energy can either augment or tamp down the spin energy of the particle. So the anti-neutron can weigh slightly more or less than the neutron.

This mass difference also ties into the color problem. In his Nobel Lecture, David Gross tells us,

Color had been introduced by O. W. Greenberg (1964), Y. Nambu (1965, 1968) and M. Y. Han and Nambu (1965). Nambu’s motivation for color was twofold; first to offer an explanation of why only (what we would now call) color singlet hadrons exist by postulating a strong force (but with no specification as to what kind of force) coupled to color, which was responsible for the fact that color-neutral states were lighter than colored states.⁴

My explanation above provides a simple mechanical cause of this mass difference, without the need of the theories that have been pasted together since the '60's. To understand both mass and chirality differences, we look at the stacked spins, and the way these four spins channel the emission. Once we understand this very powerful analysis and learn to use it, we don't need the idea of color at all.

Besides explaining mass differences, the stacked spins also explain the magnetic moment of the neutron. QCD cannot explain this in a straightforward manner. As usual, it requires a lot of ad hoc theories and new non-mechanical terms and interactions. But my spins explain it simply and immediately. Just study the stacks above, for neutron and proton. A neutron is always a proton with a reversed outer spin. Since the outer spins are reversed, the action in the magnetic field must be reversed. The magnetic field is caused by the spins on the charge photons that make up the field, and these spins must interact directly with the outer spins of baryons. This is why, if we define the magnetic moment of the proton as positive, the magnetic moment of the neutron is negative. But why is the value of the magnetic moment of the proton about 1.5x that of the neutron? Shouldn't the neutron's value be zero, since it is not emitting the charge field? No, the magnetic moment is not a measure of the baryon's own field; it is a measure of how much the baryon reacts to the given charge field that is already there. Since the neutron has a radius and a spin, it has a presence in the field. It cannot dodge the charge photons in the field, so we would not expect its magnetic moment to be zero. It value is lower than the proton because it is not emitting itself, but it is not zero. From the difference in values between the proton and neutron, we may calculate that the proton (and anti-proton) supplies about 1/3rd of the charge field at its own surface. This makes 2/3rds of the charge field ambient or residual. This will be very important in later papers.

But we still must explain the neutron’s actual decay. Why does it decay into a proton and an electron, with a bit of energy left over? Well, study the composition of the neutron and proton: all you have to do is switch the z-spin to make one into the other. So the neutron does not decay at all. No, it gets hit. It doesn’t emit the electron, it gets hit by a positron in a glancing blow, reversing the z-spin of the neutron. The collision also reverses the z-spin of the positron, turning it into an electron.

Beta decay has been misread. The detectors have failed to detect the incoming particle, and so they think it has been created. This may be because the outgoing electron follows the same path as the incoming positron, simply reversing direction. As the spin is reversed, so is the linear direction. This would "overwrite" the incoming track, making it invisible in any bubble, ionization, or other detection chamber.

From all this, one could predict that beta decay can be increased by a source of positrons of the right sort. . . except that it is already known. In reverse, this is what was happening with the 1956 experiment of Clyde Cowan, et. al. (who won the Nobel Prize for it in 1995). Beta decay was used to promote anti-beta decay. Cowan et. al. interpreted this experiment as a proof of neutrinos, but it was only a proof that the proper kind of electron in the proper B-photon field could promote anti-beta decay.

But we still must explain the neutrino. Sadly, there is no neutrino in beta decay. I know that I am taking all your prized particles from you, but that is how it goes. You can hardly complain of the large number of elementary particles, and then also complain when they are shown to be ghosts. Do you want a more elegant theory or do you not? It is like Pauli complaining that if he had known what a mess quantum physics would be, he would have gone into botany; and then adding to that mess. Pauli is responsible for this neutrino, in fact, and we have it because Pauli, like the rest, proposed a new particle to fill every hole. I am showing that we don’t need particles to fill every hole. We need logical motions and interactions.

The neutrino was proposed by Pauli to fill an energy difference. The electron plus the proton do not equal the neutron. In fact, we are about an electron and a half short, just as a matter of mass. The neutron is 2.5 electrons heavier than the proton. But all this is beside the point, since once again the historical analysis is wrong. We don’t have too little energy or mass after the decay, we have too much. If we include the energy of the B-photon field emitted by the proton, then the proton and the neutron have exactly the same mass. Before the hit, we had the neutron, and the field was internal. After the hit, we have the proton, and the field is now external, being emitted as a charge field. The electron would appear to be over the conservation line, in this sense. We have an entire electron worth of energy too much. But I have already explained that: we simply failed to detect the incoming positron. We have four types of positrons, and we have never detected the positron that causes beta decay (or at least detected its track in a beta decay experiment).

That said, we do have a failure of conservation, even given the incoming positron and the energy in the B-photon field. But this energy failure is not 1.5 electron masses. It is much smaller than that. And I will now show you both the size and the reason for the size. The standard model can tell you the first, but not the second. The standard model has no mechanical explanation for any of this.

The energy failure in beta decay is explained very simply by the energy difference between the incoming positron and the outgoing electron. Both have the same mass and the same size charge, you will say. True, but charge is no longer simply plus or minus, as I showed above. Even the charge has spin. What I mean is that the same analysis I applied to the neutron and proton must be applied to the electron and positron. The electron and positron are also emitting a B-photon field. It is about 1,836 times less strong than the field emitted by the proton, but it exists and it is repulsive. Yes, both the electron and the positron are repulsing all other particles. In that sense they both have positive charges. Look above: both the proton and anti-proton have positive charges, according to my analysis. Both are emitting and therefore repulsing, by straight bombardment. Therefore their opposite natures are not really a function of charge. They are a function of spin: the spin of the B-photons that are being emitted. Well, the same thing applies to the electron and positron. Both are emitting and therefore both are repulsing, but the B-photons of the positron are upside-down, relative to the B-photons of the electron.

Let that sink in fully, and then go back to the beta decay. The neutron becomes a proton, by switching its z-spin. This switch allows the B-photon emission of the baryon to get through. So, before the positron arrived, we had no emission from the big particle. The positron hits it, and it begins emitting. But the total B-photon field—existing after this interaction—is made up of both particles, both the baryon and the lepton. The positron’s B-photons were upside-down, relative to the proton, but the electron’s B-photons are upside-up. The positron would have subtracted from the field energy, but the electron adds to it. And so the missing energy is not in an invisible neutrino, it is in the total B-photon field. The charge of the field has appeared to go up, because the charge itself has spin. The B-photons are spinning, and we have to monitor not only the number of photons but also the spin of the photons.

This explains the experiment of 1956, since an augmented B-photon field will act exactly like a theoretical field of neutrinos. It will travel and it will carry energy. This augmented B-photon field will have exactly the right energy and spin to facilitate anti-beta decay.

It also explains neutrino oscillation, one of the major thorns of the standard model. Current theory can explain neutrino oscillation (if at all) only with ad hoc mathematical fixes. I can explain it with simple mechanics. As you see, the neutrino field is not a field of neutrinos at all. It is a field of B-photons. It is the foundational emission field in physics and the mechanical cause of E/M, with simple bombardment. In beta decay, the field emitted by the lepton inverts, due to the collision, and this changes the energy of the total field (baryon + lepton). Well, a similar thing happens in "neutrino oscillation." Neutrinos don't really change flavor, since neutrinos don't exist. What happens instead is a change in energy of the total B-photon field, and this change is due to collisions. In short, you have a series of interactions. In the first interaction, neutrons are freed from the nucleus in some manner, setting up beta decay and thereby the small rise in the B-photon field that I described above. This gives the experiment the appearance of an electron neutrino field. In the next step, the neutron is stripped of its outer spin in a second collision, turning it into a meson of one sort or another. In this collision, the baryon is stripped of its z-spin completely, and the electron is stripped of its axial and x-spins. This changes the direction of the emission field, but this is not what we are measuring after the second collision. The muon neutrino is not a field fluctuation, but the electron stripped of its spins. It takes three electron hits to strip the z-spin, and these three electrons huddle to create the muon neutrino. The muon neutrino has exactly three times the energy of a non-spinning electron, as I show in a subsequent paper. So there is no oscillation. The B-photons "oscillate"--or change their total energy--only in the first collision (notice that I am not just changing the name of the neutrino to the B-photon). The second "oscillation" is not even a measurement of a neutrino or photon field. It is an "oscillation" of the electron field.

I realize I have explained only the first and last major problems of QCD, and that there are hundreds more to solve before I convince anyone that my method is superior. But, as I said going in, my intention with this paper was not to solve every problem or to create a “final theory” of anything. My intention was to critique the current model and to suggest very strongly that a mechanical model could be and should be found. I think I have done that. I have shown that a mechanical model is not only possible, it is much simpler, much more transparent, and much more satisfying as a logical endeavor. Some will find my method naïve, but I embrace this “naivete.” It is what used to be called clarity. It is what used to be called physics.

In subsequent papers, I will take up where I left off with this one, solving each of the historical problems of nuclear mechanics in the order they arose.

For instance, one of the first things I will tackle is the problem of mesons, including the tau and the muon and their neutrinos.

For immediate gratification, you may now read my paper on Asymptotic Freedom and the Landau Pole.

And just added (12/2008) Unifying the Electron and Proton. Showing that all hadrons, mesons, and leptons are the same particle, with different spins.

The meson paper is now up (12/2008), showing the spin construction of many common mesons.

A long paper on the weak interaction is now posted (3/1/09), including a simple explanation of parity and CP symmetry.

Addendum: Some will find it premature of me to say so, but the content of this paper, along with my paper on the weak force, is already enough to bring QCD and the quark model down. This means that the entire controversy over priority, among those who won the 1979 Nobel Prize (Salam, Glashow, and Weinberg) and those who didn't (Gell-Mann, Feynman, Sudarshan and Marshak) is now moot. None of them were on the right track, and all only provided an incomplete and frankly misguided theory and math. John Gribben, a promoter of Feynman, dismissed V-A theory (Sudarshan) as "inelegant," but all the theories of that time were more than inelegant, they were wrong. The root problem of them all is that they were non-mechanical. Following the road of physics since Bohr and the Copenhagen interpretation, they were abstract and mathematical only. So, even where they were right, they were not physical. They provided no physical explanation of the data, which is what physics once was and always should be. All these various groups did is fit the data to a mathematics, which is not physics. But it is worse than that, because in fitting the data to the mathematics, they actually were forced to falsify several interactions, and to make up others. Some things they say happen don't happen in the way they claim, and others don't happen at all. For instance, they are forced to create particles that don't exist, which is a fairly large physical mistake, no matter how you look at it.

*The worst, though, are “truth“ and “beauty”, given sometimes to top and bottom quarks—Keats would be appalled.

**The Buddha would also be appalled to be included in all the dishonesty and misdirection of QCD.

¹http://en.wikipedia.org/wiki/Color_confinement

²To perform this manipulation will require different things for different people. Some will need a computer model to follow the turns; others will need math; others can do it in their heads. I almost hate to admit it, but I used a toy dog. I start with the toy facing front and traveling forward, and I imagine him spinning CW or CCW at each turn, depending on whether I am in a situation with +a or -a. Clockwise I assign to +a, and I do this simply to keep the right-hand rule. According to the right-hand rule, if you are moving forward, you are spinning CW. The right hand rule applies to electricity and magnetism, but I assume that what works for the z-spin must also work for inner spins. Here and in other places, I have given the z spin to magnetism.

³REVIEWS OF MODERN PHYSICS, VOLUME 77, JULY 2005, p. 839

⁴David Gross, REVIEWS OF MODERN PHYSICS, VOLUME 77, JULY 2005, p. 840. Or http://www.qedcorp.com/APS/DGNobelRevModPhys_77_000837.pdf

⁵See my newer paper The Infinite Weakness of the Theory of Weak Interaction for a fuller explanation of how and why gauge math fails.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.