return to homepage HOW TO BUILD A NUCLEUS
return to updates
without a Strong Force
by Miles Mathis
milesmathis.com
mm@milesmathis.com
Contemporary physics has sold us a quantum interaction called the strong force, which is supposed to be one of the four fundamental forces of nature. This interaction has been forced down our throats despite the known fact that there is no evidence for it. The strong force is just a theory. It is a theoretical force proposed to counteract E/M repulsion in the nucleus. Problem is, quantum physicists have never proved that there is an E/M repulsion in the nucleus. They have simply assumed that there is. Because the E/M field is known to be ubiquitous at the macro-level, quantum physicists have assumed from the very beginning that it must be present in the nucleus. If it is present, it must be overcome, to explain the nearness of nucleons to one another.
Now that we have a new model of the nucleus, we find that many things are different than before. Not only have we bypassed the need for a strong force, we have completely overturned the old model of the nucleus as a round-ish collection of nucleons, crammed together willy-nilly. The nucleus is not a formless conglomeration, like a bag of marbles, it is a well-defined stack, with many rules of stacking. Beyond that, the nucleus can no longer be considered a simple ion, seeking electrons. It must now be considered a very complex engine. Why is it an engine, you may ask? Well, notice that the stack of protons still has a hole top and bottom. It has charge minima at both ends of the stack. These holes act as intake valves, through which the nucleus can capture other quanta. We may imagine that it can capture anything from photons up to electrons, and possibly even larger quanta. What does it do with these captured particles? It “burns” them, recycling them into a new charge field that it can re-emit. Just as I have already shown how other quanta are engines in this way, the nucleus is just a bigger engine. A single proton, for instance, is already an engine, since it can re-process the charge field through these charge holes, feeding off the charge field and quantum field and then excreting the charge field by flinging it off via its rotation. This explains where the charge field comes from: we do not need to theorize that it is created from nothing by the proton, we simply allow that it is infinitely recycled. The same thing applies to the nucleus. The nucleus can also capture its own charge field through these charge minima and then re-emit it.
But I will show that the E/M field is not present within the nucleus in the way we have been told. This means that the strong force is one more theoretical and mathematical ghost.
To prove this, I will actually show you how to build a nucleus without the strong force. I will diagram several nuclei, showing that it is quite easy to construct a model of protons and neutrons in which all E/M emission is external.
To achieve this requires only a few simple postulates. The first postulate is that the E/M field is caused by an emission field. Protons must be emitting something in order to create the repulsion. The standard model already accepts this postulate, in a mutated and illogical form. The standard model proposes that charged particles emit virtual or messenger photons which are capable of telling other quanta to move away or move closer. Since this proposition is non-mechanical, non-physical, and magical, and since my papers are concerned with physics and mechanics, I must bring this proposition back in line with logic and physics. To do that, I only have to get rid of the “messenger” or “virtual” part of the theory. I propose that protons emit real photons, and that these real photons cause repulsion by simple bombardment. Since we are dealing with protons and neutrons here, but not electrons, I do not have to explain charge attraction. When speaking of nuclear forces and interactions, charge attraction is not a concern. However, I have explained charge attraction in many other places.
The second postulate is that quanta are spinning. Again, the standard model already accepts this postulate in a mutated and illogical form. Quanta are given various quantum numbers called spin or angular momentum and so on, but then the standard model denies that quanta are spinning physically. We are told that they are point particles, and that the numbers are mathematical in nature, not physical in nature. As a matter of physics, this must be a strange assertion, but it is an axiom of contemporary physics. Students of physics are warned, in very serious tones, not to try to diagram or imagine anything at the quantum level. We are told that the quantum arena is inherently strange and mysterious, not amenable to logic or reason. As a matter of job protection, that is an understandable warning; as a matter of physics, it is just silly.
I return to logic, and logic states that if quanta exist, they have extension. If they have extension, they may have real angular momentum or spin. This angular momentum can then be analyzed just like angular momentum at the macro-level. This applies to all quanta, even the smallest. Photons have real spin just like planets or stars or galaxies. But here, we only need postulate that the nucleons are spinning. We know that nucleons have appreciable size, especially compared to photons, so that postulate is not difficult to make. Nucleons are huge compared to photons or electrons, so why not diagram them with spin?
In fact, I have already shown that baryons (protons and neutrons) have four stacked spins. These stacked spins are fully capable of explaining all the characteristics now given to quarks, without a quark model. It is these spins which will allow me to build the nucleus without the strong force.
To begin, we will look only at the outer or z-spin of the baryon. The proton and neutron are both spinning, and since they are approximately the same size, their z-spins will have approximately the same angular momentum. What makes the two particles so different is that the proton is emitting a charge field and the neutron is not. The neutron is swallowing its charge field, since the photons cannot navigate the maze of spins. The four spins of the neutron bring the photons back to the center, while the four spins of the proton allow the photons to escape. I have diagrammed this in previous papers. What this means for our analysis here is that the proton must be treated as an extended particle, while the neutron is treated as a discrete particle. In other words, in this first part of the analysis, the neutron is treated mainly as a z-spin, while the proton is treated as a z-spin plus the shell of emitted photons.
To visualize this easily, think of a lawn sprinkler, one that spins like a pinwheel. The neutron is like the lawn sprinkler spinning, but without the water. The proton is like the lawn sprinkler plus the water being emitted. In this way, the proton acts like a much larger particle, and that is how we will diagram it. You see, to make sense of the nucleus, I must diagram both the particles and the charge field. To do this, I will have to give the charge field both a presence and a direction at all points.
As the next step, we will have to represent the nucleons in some simplified way. Since the nucleons are spinning, we may simplify the sphere into a circle. To justify this, I will ask you to first imagine a sphere emitting a field in all directions. Then, let this sphere spin about a N-S axis, like the Earth. Due to centrifugal forces, nearly all the emission will now be moving in a direction out from the equator. Almost none will be emitted N-S. To put it another way, the emission field of this spinning sphere will have developed large holes at the north and south poles. If the emission field is a charge field, then the charge field will have large minima in the north and south directions. In fact, the spinning sphere will act very much like a spinning disk, with most of the charge being emitted equatorially. The faster the sphere is spinning, the more it will act like a disk. For this reason, in a simplified diagram we can treat the proton as a disk. As a matter of its charge field influence on surrounding bodies, the proton acts much like a circle or disk, which helps when we need to diagram it on a piece of paper.
The same analysis can be applied to the neutron, since it is also spinning. The z-spin causes most of the angular momentum of the neutron to be expressed equatorially, so we can also treat the neutron as a circle.
With these postulates in hand, we are now ready to look at the simplest nucleus with more than one nucleon: helium. We know that helium has an atomic weight of about 4, with two protons and two neutrons, but the standard model has never told us clearly and distinctly why that is so. Why doesn't helium just have two protons? Or, why not 1 neutron or 3 or 4 or any other number? Why is the atomic number 4 stable? The standard model avoids questions like this with much misdirection and disinformation, but I can answer it with very simple mechanics and clear diagrams.
Since I have already shown that the spinning protons must have large charge holes north and south, we simply let the protons meet hole to hole. When helium is created by pressure (as in a star or Big Bang), these holes naturally align. Once the pressure is turned off—when the matter escapes the star—the alignment either persists, because it is in a stable form, or it decays, because it is not.
Two protons hole to hole align naturally under pressure, since this is the lowest energy state, but once the pressure is turned off, the two protons are again free to turn. If the two proton disks start to turn, the two charge fields hit eachother and we have repulsion. The two protons together are not stable, even when originally aligned hole to hole, since there is nothing to prevent them from drifting and turning. But if neutrons are present in the star, and if they happen to be present in the right places, they can provide this stability. This is quite easy to diagram:
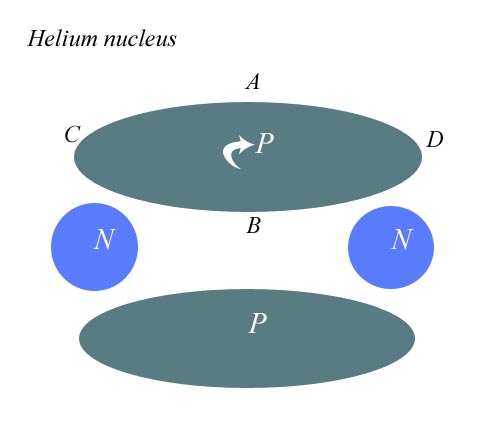
As you see, the neutrons act like little pillars or posts, keeping the proton disks from turning and repulsing one another.
You will say, “Don't we need at least four posts to keep the protons from turning toward eachother? Can't the proton disks still fall together at points A and B?”
No, we don't, and they can't. You would be correct, if the disks were not spinning. But because they are spinning, stability can be created by only two posts. For the disks to fall together at point A, say, would require a point on the edge of the disk to be high at point C, low at point A, and high again at point D. To do this, the disk would not “fall”, it would warp. We have simplified our sphere into a disk, not into a floppy hat.
My assumptions here are very normal, and you can test them in real experiments with real disks. Spinning disks can be kept apart, in permanent stability, by two posts, as I have diagrammed it.
Since that is true, I have already proved my point with regard to helium. As you can see from the same diagram, no charge is being emitted into the nucleus. All charge is being emitted to the outside. We may assume that some tiny fraction of charge force is being felt by the neutrons, although they are orthogonal to the main line of charge. They could not provide stability if they did not resist turning, and they could not resist turning except by mechanical means. But we will assume that the angular momentum of the neutrons is more than enough to offset this small amount of charge encountered. Using commonsense mechanical postulates, we see that the bulk of the charge is emitted outside the nucleus. Therefore we have no need for the strong force in the helium nucleus.
We can apply the same analysis to lithium. We have three protons and four neutrons. We stack our three disks, and need four posts to separate them.
But now we arrive at the beryllium nucleus. In this case we have four protons and five neutrons. Why that number? Why is the number 9 stable when the numbers 8 and 10 are not? If we use the same diagram as we used for helium and lithium, we would expect to need 6 neutrons to separate 4 protons, which would give us 10. Obviously, the nucleus has already discovered a more efficient method than our dual posts. Beryllium 10, with 6 neutrons, is actually very stable, with a half life of over a million years, so nature does use the six post model here. But the five post model is also effective, so given the chance, nature will prefer it. Beryllium can stack with only five posts due to the fact that the lithium model is already so stable. If we place the neutrons in lithium like this,

then we have such a solid spinning structure that the top level can be balanced by only one neutron, placed in the middle. The disk below cannot turn, so the central neutron must resist only the upper disk. Remember that the neutron is not a narrow pillar. It has a z-spin radius equal to that of the proton, so it is quite capable of providing stability in this way. If we let it spin in the same plane as the protons, this is even more obvious.
You will say, “Well, if we can balance disks so easily, why did we not let one neutron balance the third proton in lithium? Weren't the first two disks almost as stable?” Yes, they were, and we can. Lithium 6 is a stable isotope, existing abundantly in the universe. The reason it isn't as common as lithium 7 is probably due to the fact that it is burned more easily in stars. It is slightly easier to break that one post than the two posts of lithium 7, so stars will burn lithium 6 preferentially.
The same analysis applies to helium 3. Helium 3 is stable, but easier to burn than helium 4.
Our stacking method also explains boron, since we use the one post top and bottom, giving us five protons and six neutrons. As expected, boron 10 is also stable, but it likes to capture an extra neutron to achieve even more symmetry and stability.
With all the smaller elements, this disk stacking is both simple and intuitive. And, as you can see, it continues to keep the E/M field out of the nucleus, even as we go down the periodic table.
If this is true, then the various quantum beasts, including the periodic zoo of nuclei, are not only engines, they might almost be called alive, since they eat and excrete the charge field. Not only that, but they eat and excrete one another. The protons and nuclei aren't just passive valves through which pass the photons of the charge field. No, it appears that the protons and nuclei can eat electrons as well, digesting them by stripping off outer spins, and turning them into charge photons. Yes, a certain number of lucky electrons get caught in the whirlpool, and achieve a limited stability in the shells. But any electrons too high or too low for the whirlpool get sucked into the charge minima at the ends of the nucleus, and are turned into photons.
Our new model of the nucleus as a stack rather than a ball also helps us explain the relative paucity of elements. With the ball model, it is not clear why we cannot continue to add nucleons. Adding more marbles to a bag of marbles does not increase its instability or decrease its likelihood of existence. But with the stack model, it is clear that a larger stack implies a greater instability. For two reasons: 1) the stack becomes less probable the larger it gets, just as a matter of statistics. The neutrons have to arrive in the proper places at the proper times, in a fixed method, and this method becomes less probable with each added nucleon; 2) just as with a stack of plates, a stack of nucleons must become more unstable at greater numbers. To start with, the expanding length of the nucleus must encounter a larger cross section of the charge field, opening the larger nucleus up not only to photon wind variations, but to more quantum collisions of all kinds. As we know, a sphere is the most stable configuration of volume. A stack is among the least stable, at all levels of size. This must strongly prejudice nature in favor of the short stack.
In a newer paper, I address some of the anomalies of the Periodic Table, including the radioactivity of technetium and promethium, and of all isotopes above number 83. I will show why the numbers 43 and 61 fail to be stable at any weight, and this will provide us with more rules of stacking. I will show that the baryons actually channel charge through the nucleus, updating this paper. Charge does exist in the nucleus, but it is channeled to prevent repulsion and to prevent, in many cases, radioactivity. Diagrams of the larger elements show how this is done, and prove once more that the strong force is not needed. I also show that the basic electron orbitals are wrong. Subsequent papers on Uranium and the Lathanides also prove this.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.